1. S=1/2*a*h
h=18, найдем а=18/3=6, подставляем S=1/2*6*18=54cм².
2. Площадь прямоугольного треугольника вычисляется по формуле
S=1/2*a*b (a,b - катеты). Пусть а=20, тогда в=2/5*20=8см. Подставим значения: S=1/2*20*8=80 см².
3.Формула S=1/2*d1*d2. Подставляем значения S=1/2*10*8=40cм².
Формула периметра по диагоналям: Р=4√(d1÷2)²+(d2÷2)²
подставим значения Р=4√(10÷2)²+(8÷2)²=4√5²+4²=36 см.
4. Формула площади параллелограмма: S=1/2*a*h. Построим высоту h. Из условия видим , что h-катет, противолежащий углу 30° ⇒ он равен половине гипотенузы, значит h=30÷2=15см. Подставляем значения в формулу площади S=1/2*52*15=390см².
5.Формула площади трапеции : S=1/2*h*(a+b)
в=15см-большее основание, тогда а=15-5=10см-меньшее основание, вычислим высоту h=15÷3=5. Подставим значения S=1/2*5*(15+10)=62.5cм²
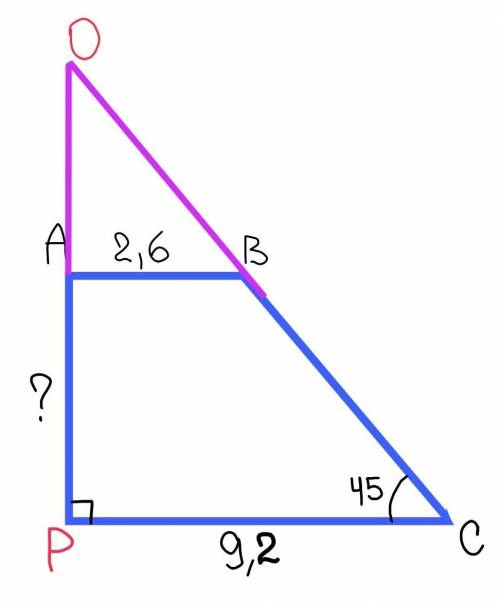
Продлим РА за точку А и СВ за точку В, точку пересечения назовём О.
∆РОС – прямоугольный с прямым углом Р.
Сумма острых углов прямоугольного треугольника равна 90°. Исходя из этого: угол РОС=90°–угол ОСР=90°–45°=45°.
Получим что угол РОС=угол ОСР, тогда ∆РОС – равнобедренный с основанием ОВ.
Тогда РО=РС=9,2 см.
Основания трапеции параллельны, тоесть АВ//РС.
Следовательно: угол ОВА=угол ОСР как соответственные при параллельных прямых АВ и РС и секущей ОС; тогда угол ОВА=45°.
Угол АОВ=45° (доказано ранее)
Получим что угол ОВА=угол АОВ.
Тогда ∆АОВ – равнобедренный с основанием ОВ. Следовательно АО=АВ=2,6 см.
РА=РО–АО=9,2–2,6=6,6 см.
ответ: 6,6 см.
h1=5 см h2=7.5см
Объяснение зробимо малюнок , з якого все видно: