Найдите длину окружности , описанной около:
1)прямоугольника, меньшая сторона которого равна 8 см, а угол между диагоналями равен α;
2)правильного треугольника, площадь которого равна 48√3 см²
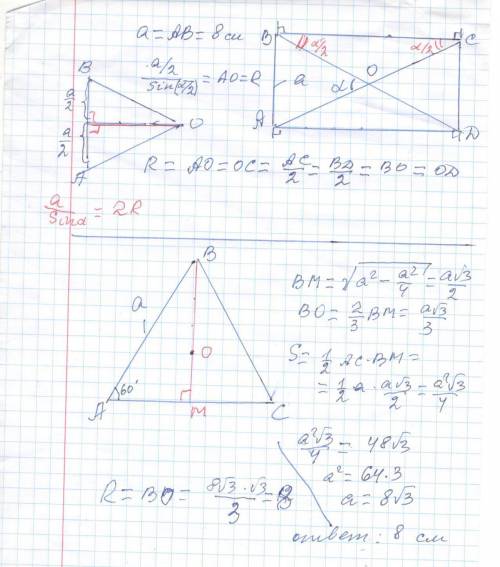
1) R = AC/2 * * * R =d/2 = AC/2 =AO * * *
Из ΔABC: AC =2*AO =AB /sin(α/2) =8/sin(α/2)
R = 4/sin(α/2)
2) a/sinα =2R ⇒ R = a/2sinα =a/2sin60° =a/(2*√3 /2) = a /√3 || (a√3)/3 ||
* * * S = (1/2)*absinC * * * S = (1/2)*a*a*sin60° =(a²√3) / 4
48√3 =(a²√3) / 4 ⇔a²/ 4 = 48 ⇔a² =4*48 = 4*16*3 ⇒ a=8√3
R = a /√3 = 8√3/√3 =8
Первый .
Для решения применим теорему косинусов для треугольника.
ВС2 = АВ2 + АС2 – 2 * АВ * ВС * CosA.
ВС2 = 9 + 36 – 2 * 3 * 6 * (1 / 2).
ВС2 = 45 – 18 = 27.
ВС = √27 = 3 * √3 см.
Второй .
Проведем высоту ВН.
В прямоугольном треугольнике АВН катет АН лежит против угла 300, тогда АН = АВ / 2 = 3 / 2 = 1,5 см. СН = АС – АН = 6 – 1,5 = 4,5 см.
Тогда ВН2 = АВ2 – АН2 = 9 – 2,25 = 6,75.
В прямоугольном треугольнике ВСН, ВС2 = ВН2 + СН2 = 6,75 + 20,25 = 27.
ВС = √27 = 3 * √3 см.
ответ: Длина стороны ВС равна ВС 3 * √3 см.
Объяснение: