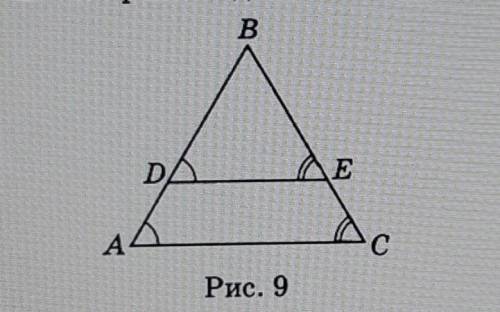
Объяснение:
1) Так как угол bde =углу bac ( по условию ) , то они являются соответствующими , то DE параллельно AC.
2)Прямая , параллельная стороне треугольника , отсекает от него треугольник подобный данному .
3) Треугольник ABCравнобедренный , потому что АВ=АС(по условию)
значит угол А= углу С и по свойствам подобных треугольников угол A=D=E=C
Что и требовалось доказать
Рассмотрим трeугольники BCO и ABO:
BO - общая, угол COB=AOB, CO=OA( по условию)
Следовательно СOB=AOB
Значит, если они равны, то все их углы и стороны соотвественно равны, то есть BC=BA. Получается, что треугольник CBA-равнобедренный. Прямая BO-высота и серединный перпендикуляр т.к. по св-ву равнобедренного треугольника высота является медианой и биссектрисой.ч.т.д.
1) Первый Рассмотрим треугольник BB1A (пусть B1 - точка лежащая на пересечении прямой со стороной AC). Угол BB1A=90 градусов. Следовательно угол B1BA= 90-55=35.
Т.к. треугольник CBO=AOB, угол OBA=OBC=35 градусов. Угол CBA= 35+35=70 гр
Следовательно угол BCA=180-угол CAB-угол ABC=180 гр-55гр-70 гр=55 гр
2) Второй т.к BCA-равнобедренный, следовательно углы при основании у него равны. Угол CAB=BCA=55 гр
ответ:55 гр
a) угол В = 38
рассм. ABC: угол A=90, угол B=38 ⇒ угол С=52
рассм. ABH: угол H=90. угол B=38 ⇒ угол A=180-90-38=52
рассм. AHC: угол H=90. угол С=52 ⇒ угол A=38
угол HAM = 52-38 = 14
углы 52, 14 и 38
б) угол B = 20
рассм. ABC: угол A=90, угол B=20 ⇒ угол С=70
рассм. ABH: угол H=90. угол B=20 ⇒ угол A=180-90-38=70
рассм. AHC: угол H=90. угол С=70 ⇒ угол A=20
угол HAM = 70-20 = 50
углы 20, 50 и 70
в) угол HAM = 42
рассм HAM: угол H = 90, угол A=42 ⇒ угол M=48
рассм AMC равнобед. : угол M = 180-48 = 132 ⇒ угол A = C = (180-132)/2 = 24
угол CAH = 42+24=66
угол BAH = 90-66=24
углы 24,42,24
г) угол B = a
рассм. ABC: угол A=90, угол B=a ⇒ угол С=90-a
рассм. ABH: угол H=90. угол B=a ⇒ угол A=90-a
рассм. AHC: угол H=90. угол С=90-a ⇒ угол A=90-(90-a)=a
угол HAM = (90-a)-a=90-2a
углы a. 90-a. 90-2a
далмьлвлвлсллабсьмьпт