
В треугольнике ABC, AB = BC. Медианы треугольника пересекаются в точке O, OA = 5, OB = 6. Найдите площадь треугольника ABC.
============================================================
точка О - точка пересечения медиан ( см приложение )По свойству пересечения медиан в ΔАВС ВО:ОЕ = 2 : 1⇒ ОЕ = ВО/2 = 6/2 = 3 По свойству равнобедренного треугольника ВЕ⊥АС, ВЕ - медиана, высота, биссектрисаВ ΔАОЕ: по теореме ПифагораАЕ² = АО² - ОЕ² = 5² - 3² = 25 - 9 = 16АЕ = 4АС = 2•АE = 2•4 = 8Значит, S abc = BE•AC/2 = 9•8/2 = 36ОТВЕТ: S abc = 36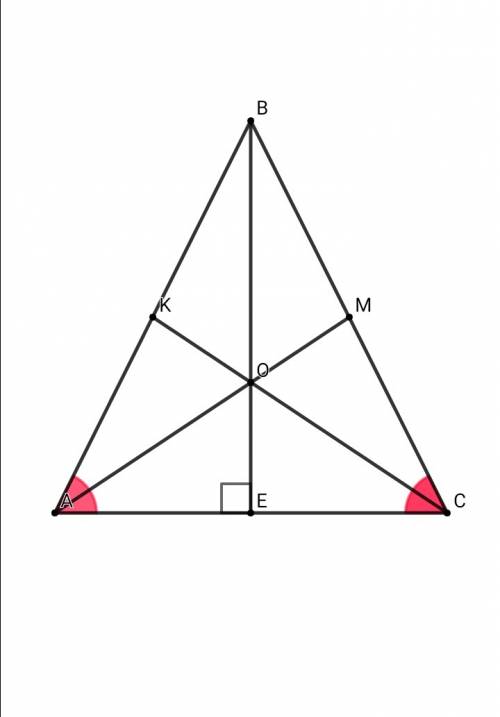
Пусть AB = c; BC = a; АС = b (задано, b = 12*корень(2)); AM = MC = b/2; угол МВС = Ф;
Из теоремы синусов для тр-ка ВМС (R1 - радиус описанной окружности, R1 = 2*корень(6);)
2*R1*sin(Ф) = b/2; отсюда sin(Ф) = b/(4*R1);
Из теоремы синусов для тр-ка ВМA (R2 - радиус описанной окружности, R2 надо найти; В - это угол АВС = 150 градусов)
2*R2*sin(В - Ф) = b/2; отсюда R2 = b/(4*sin(B - Ф));
На самом деле это уже ответ.
Но для полноты картины надо подставить числа и максимально упростить.
Для начала видно, что
sin(Ф) = 12*корень(2)/(4*2*корень(6)) = корень(3)/2.
Угол с таким синусом в треугольнике может быть либо 60 градусов, либо 120 (соответственно, cos(Ф) принимает значение либо 1/2 либо (-1/2); )
Если Ф = 60 градусов, то В - Ф = 90 градусов, sin(В - Ф) = 1; и R2 = b/4 = 3*корень(2);
Если Ф = 120 градусов, то В - Ф = 30 градусов, sin(В - Ф) = 1/2; и R2 = b/2 = 6*корень(2);
У меня получилось 2 решения.