130°
Объяснение:
Сумма острых углов прямоугольного треугольника равна 90°.
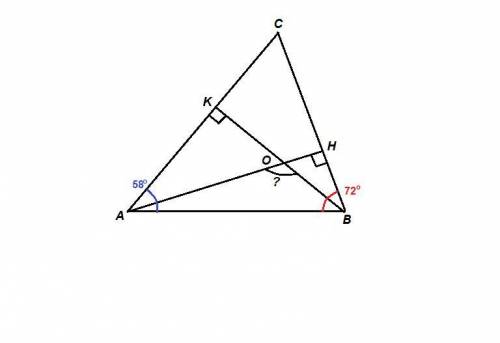
ΔАНВ: ∠ АНВ = 90°,
∠ВАН = 90° - ∠АВН = 90° - 72° = 18°
ΔВКА: ∠ВКА = 90°,
∠АВК = 90° - ∠ВАК = 90° - 58° = 32°
ΔАОВ:
∠АОВ = 180° - (∠ВАО + ∠АВО) = 180° - (18° + 32°) =
= 180° - 50° = 130°
Из ΔАВС:
∠С = 180° - (∠А + ∠В) = 180° - (58° + 72°) = 180° - 130° = 50°
Сумма углов выпуклого четырехугольника равна 360°.
Для четырехугольника СКОН:
∠КОН = 360° - (∠С + ∠К + ∠Н) = 360° - (50° + 90° + 90°) =
= 360° - 230° = 130°
АКВ = 140°.
Объяснение:
Угол АОВ - центральный => дуга АКВ равна градусной мере угла АОВ, то есть 80°.
Градусная мера дуги АВ равна 360° - 80° = 280°.
Соединим точку К с точками А и В.
Угол АКВ - вписанный, опирающийся на дугу АВ и равен половине градусной меры дуги, на которую он опирается, то есть ∠АКВ = 140°.