Запишите уравнение прямой, симметрично прямой y = x - 2 относительно точки A(-3;1)
Объяснение:
Прямая y = x - 2, к=1 ; К(0; -2) принадлежит этой прямой( легко проверяется) .
Пусть уравнение симметричной прямой у₁=к₁х+в₁ .
Т.к прямые симметричные относительно точки, то они параллельны ⇒ их угловые коэффициенты равны , значит к₁=1. Пусть К₁∈у₁ .
Найдем координаты точки К₁(х;у) симметричной точке К( 0;-2) относительно A(-3;1) , по формулам середины отрезка ( тк.АК=АК₁)
х(А)= , x(K₁)=-3*2-0=-6,
y(A)= , y((K₁)= 1*2-(-2)= 4 ⇒ K₁(-6; 4 ).
В уравнение у₁=к₁х+в₁ подставим к=1 и K₁(-6; 4 ) , получим 4=1*(-6)+в₁,
в₁=10 . Окончательно получаем у₁=1х+10 или у₁=х+10.
Запишите уравнение прямой, симметрично прямой y = x - 2 относительно точки A(-3;1)
Объяснение:
Прямая y = x - 2, к=1 ; К(0; -2) принадлежит этой прямой( легко проверяется) .
Пусть уравнение симметричной прямой у₁=к₁х+в₁ .
Т.к прямые симметричные относительно точки, то они параллельны ⇒ их угловые коэффициенты равны , значит к₁=1. Пусть К₁∈у₁ .
Найдем координаты точки К₁(х;у) симметричной точке К( 0;-2) относительно A(-3;1) , по формулам середины отрезка ( тк.АК=АК₁)
х(А)= , x(K₁)=-3*2-0=-6,
, x(K₁)=-3*2-0=-6,
y(A)=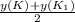 , y((K₁)= 1*2-(-2)= 4 ⇒ K₁(-6; 4 ).
, y((K₁)= 1*2-(-2)= 4 ⇒ K₁(-6; 4 ).
В уравнение у₁=к₁х+в₁ подставим к=1 и K₁(-6; 4 ) , получим 4=1*(-6)+в₁,
в₁=10 . Окончательно получаем у₁=1х+10 или у₁=х+10.