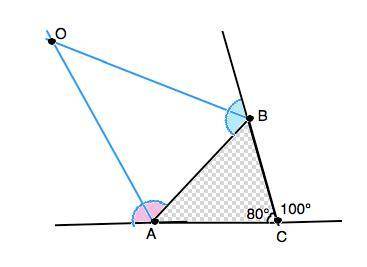
В треугольнике АВС угол С=80°. Найдите градусную меру угла АОВ, если О -точка пересечения биссектрис внешних углов треугольника при вершинах А и В.
Ответ: 50°
Объяснение: Сумма внешних углов многоугольника, взятых по одному у каждой вершины, равна 360°.
Внешний угол при С равен 180°-80°=100°. На сумму внешних углов при А и В приходится 360°-100°=260°.
Тогда в треугольнике АОВ сумма углов при вершинах А и В равна половине суммы внешних углов при А и В треугольника АВС, Т.е. ∠ОАВ+∠ОВА=260°:2=130°
Из суммы углов треугольника угол АОВ=180°-130°=50°
Объяснение:
1.
По заданию видно, что стороны АД и ДВ равны, следовательно треугольник АДВ равнобедренный, по его свойствам углы у основания равны, значит углы ДАВ и ДВА равны, ДАВ=ДВА= 70°
ответ. 70°
2.
По заданию видно, что стороны АС и АВ равны, следовательно треугольник АВС равнобедренный, по его свойствам углы у основания равны, значит углы АСВ и АВС равны, АСВ=АВС= 70°.
Углы АВС и АВД смежные, а сумма смежных углов равна 180°, следовательно угол
ДВА= 180-АВС= 180-70=110°
ответ. 110°
3. По заданию видно, что стороны КС и КВ равны, следовательно треугольник КВС равнобедренный, по его свойствам углы у основания равны, значит углы КСВ и КВС равны, КСВ=КВС= 70°.
Углы СВК и ДВА вертикальные, а вертикальные углы равны, следовательно СВК=ДВА=70°
ответ. 70°
ответ:1) пусть ВС-х, тогда АС х+5, отсюда уравнение: х+х+5=20; 2х=15; х=7,5(см)ВС, 7,5+5=12,5(см)АС 2)пусть АС х, ВС 4х, тогда:х+4х=20; 5х=20; х=4(см) АС, 4×4=16(см)ВС.
Объяснение: