точка S знаходиться на одній відстані від усіх вершин правильного трикутника зі стороною 2 корінь з 3 см і відалена від площини трикутника на корінь з 3 см знайдіть відстань від точки S до вершини трикутника.
Точка S находится на одном расстоянии от всех вершин правильного треугольника со стороной 2 корня из 3 см и відалена от плоскости треугольника на корень из 3 см найдите расстояние от точки S до вершины треугольника.
Объяснение:
Т.к. точка S находится на одном расстоянии от всех вершин правильного треугольника, то SA=SB=SC.
Расстояние от S до плоскости ( АВС) √3 см⇒SO⊥(АВС). Тогда прямоугольные треугольники равны по катету (SO-общий) и гипотенузе ( SA=SB=SC.) ΔSOA=ΔSOB=ΔSOC ⇒ОА=ОВ=ОС и значит О-центр описанной окружности около правильного ΔАВС и ОА=ОВ=ОС=R = ,
R = =2 (см)
ΔSOA- прямоугольный , по т. Пифагора SA= √(2²+√3²)=√7 (cм)
(х-а)²+(у-в)²=R²- уравнение окружности где (а;в)-координаты центра окружности R--радиус (х-2)²+(у-3)²=4² (х-2)²+(у-3)²=16 начало координат имеет координаты О(0;0) (х-0)²+(у-0)²=(5/2)² x²+y²=25/4 (R=5/2) X²+y²=25 (R=5) 2. C x=(2+4)÷2 y=(7+5)÷2 x=3 y=6 C (3 ; 6) координаты середины отрезка находятся за формулой х=(х1+х2)÷2; у=(у1+у2)÷2 где (х1; у1) (х2;у2) координаты конца отрезка АВ ((4-2); (7-5)) АВ (2;2) АВ²=(4-2)²+(7-5)²=2²+2²=4+4=8 АВ=√8=√4·2=√2²·2=2√2 y=kx+b уравнение прямой если прямая проходит через точки значит ее координаты удовлетворяют уравнение прямой 5=2k+b (×-1) -5=-2k-b 7=4k+b первое уравнение + второе 2=2k k=2/2=1 5=2·1+b b=5-2=3 y=x+3 уравнение прямой которая проходит через точки А и В
Ну, в треуг. к бОльшей стороне проводится мЕньшая высота. Док-во очень простое, логическое. Площадь треуг.- величина постоянная? Да. Тогда если брать произведение бОльшей стороны на какую-то высоту (1) и мЕньшую сторону на какую-то высоту (2), то понятно, что (1) должна быть меньше (2) Соответственно 10 - 9 15 - 6 18 - 5 Проверяя по площади, находим, что это так.
Но вот только неувязочка с задачей- высоты -то фейковые! Из решения получаем, что площадь треуг. будет, например , 10*9/2=45
А из сторон 15,18 и 10 по формуле Герона находим истинную площадь - приблизительно 75. Тем, кто составлял условие задачи - руки повыдергивать. Так учителю и скажи.
Точка S находится на одном расстоянии от всех вершин правильного треугольника со стороной 2 корня из 3 см и відалена от плоскости треугольника на корень из 3 см найдите расстояние от точки S до вершины треугольника.
Объяснение:
Т.к. точка S находится на одном расстоянии от всех вершин правильного треугольника, то SA=SB=SC.
Расстояние от S до плоскости ( АВС) √3 см⇒SO⊥(АВС). Тогда прямоугольные треугольники равны по катету (SO-общий) и гипотенузе ( SA=SB=SC.) ΔSOA=ΔSOB=ΔSOC ⇒ОА=ОВ=ОС и значит О-центр описанной окружности около правильного ΔАВС и ОА=ОВ=ОС=R =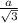 ,
,
R =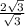 =2 (см)
=2 (см)
ΔSOA- прямоугольный , по т. Пифагора SA= √(2²+√3²)=√7 (cм)