Есть две окружности. условия: 1) радиус первой окружности является диаметром для другой; 2) через конец второго радиуса этой окружности проведена касательная к меньшей с точкой касания, отличной от данного конца; 3) перпендикуляр вышеуказанного второго радиуса, проведенный через другой его конец, пересекает меньшую окружность в вышеупомянутой точке касания; найдите угол между между данными радиусами в градусах с точностью до семи значащих цифр.
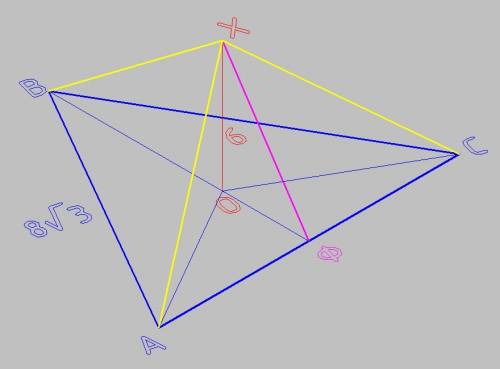
Известна сторона основания а = 8√3 ≈ 13,856406 см.
Известна высота пирамиды Н = 6 см.
tg α Угол накл. боков. грани к основан. α=arc tg1.5 =
0,982794 радиан = 56,309932 градуса.
tgβ Угол накл. боков. ребра к основ. β = arc tg 0.75 =
= 0,643501 радиан =36,869898 градуса.
Высота треугольника в основании h = a*cos30 = 12 см
Площадь основания So = а²√3/4 = 83,138439.
Периметр Р = 3а = 41,569219.
Площадь бок.пов. Sбок = (1/2)РА = 149,87995.
Апофема А = 7,2111026.
Полная поверхность S = 233,0184 см².
Бок.ребро L = 10.
Объём V = 166,2769 см³.
Основа решения - свойство правильной треугольной пирамиды:
проекция бокового ребра на основание равн(2/3) высоты h основания, а проекция апофемы - (1/3)h.