Из прямоугольного треугольника ABD
AD^2=AB^2+BD^2=9+16=25
AD=5
Площадь основания равна 2*площадь ABD=2*(3*4/2)=3*4=12
AD параллельно BC, следовательно параллельно B1C1, поэтому AD принадлежит плоскости AB1C1, и это прямая пересечения плоскости основания с плоскостью AB1C1
Пусть BE высота в треугольнике ABD
Тогда угол B1EB это угол между плоскостью основания и плоскостью AB1C1, так как BE перпендикулярно AD, B1E перпендикулярно AD по теореме о трёх перпендикулярах.
Треугольник B1EB -- прямоугольный треугольник с углом 45 градусов, а следовательно, равнобедренный прямоугольный треугольник, поэтому B1B=BE
Чтобы найти высоту BE выразим площадь треугольника ABD двумя
площадь ABD = AB*BD/2 = AD*BE/2, отсюда
BE=AB*BD/AD=3*4/5=12/5=2,4
Площадь полной поверхности равна
2*площадь основания+площадь боковой поверхности
площадь боковой поверхности = периметр основания умножить на высоту
периметр основания = AB+BC+CD+AD=3+5+3+5=16
тогда площадь боковой поверхности 16*2,4=38,4
площадь полной поверхности
2*12+38,4=24+38,4=62,4
108°, 60°, 12°
Объяснение:
Внешний угол треугольника равен сумме двух внутренних углов не смежных ним:
<1=<В+<С
<2=<А+<С
<3=<А+<В
отсюда сумма внешних углов треугольника взятых по одному при каждой вершине равна:
<1+<2+<3=<В+<С+<А+<С+<А+<В=2(<А+<В+<С)
Так как сумма углов треугольника равна 180 градусов то <А+<В+<С=180°.
Значит <1+<2+<3=2×180°=360°
Пусть:
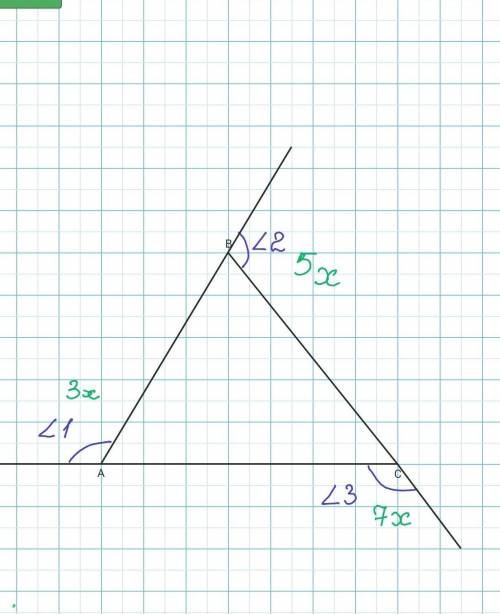
<1=3х
<2=5х
<3=7х
Составляем уравнение:
3х+5х+7х=360
15х = 360
х = 24
<1=3х=3×24=72°
<2=5х=5×24=120°
<3=7х=7×24=168°
Так как внешний угол треугольника - это угол смежный с внутренним углом треугольника, а сумма смежных углов равна 180° то
<А= 180°-<1=180°-72°=108°
<В=180°-<2=180°-120°=60°
<С=180°-<3=180°-168°=12°
Адамдар мен жылықанды жануарлар
Объяснение: