Сумма углов треугольника на евклидовой плоскости равна 180°.
Из теоремы следует, что у любого треугольника не меньше двух острых углов. Действительно, применяя доказательство от противного, допустим, что у треугольника только один острый угол или вообще нет острых углов. Тогда у этого треугольника есть, по крайней мере, два угла, каждый из которых не меньше 90°. Сумма этих углов не меньше 180°. А это невозможно, так как сумма всех углов треугольника равна 180°.
Обънайдем середины отрезков:
1) точка К на отрезке АС: К(-2+0/2;2+0/2) = K(-1;1)
уравнение медианы ВК: х-х1/х2-х1 = у-у1/у2-у1
х-1/-1-1 = у-2/1-4 = 3х-2у + 1 = 0
2) тока L на отрезке АВ: L(-0,5;3)
уравнение медианы CL: х-0/0,5-0 = у-0/3-0 = 3х +0,5у=0
3) точка M на отрезке ВС: M(0,5;2)
уравнение медианы АМ: х+2/0,5+2 = у-2/2-2
х+2/2,5 = 1, х = 0,5
!!!уравнение сторон:
уравнение стороны АВ: х+2/3 = у-2/2 = 2х-3у+10 = 0
уравнение стороны АС: х+2/0+2 = у-2/0-2 = 2у-2х = 0
уравнение стороны ВС: х-1/0-1 = у-4/0-4 = 4х-у = 0
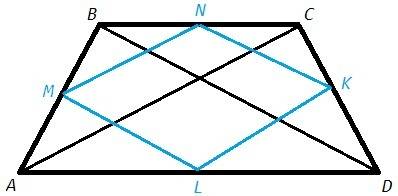
Середины сторон четырехугольника являются вершинами параллелограмма (теорема Вариньона). Стороны параллелограмма Вариньона параллельны диагоналям четырехугольника и равны их половинам (т.к. являются средними линиями в треугольниках, образованных сторонами и диагоналями).
Диагонали равнобедренной трапеции равны, следовательно стороны параллелограмма Вариньона равны и он является ромбом.
MN - средняя линия в ABC => MN||AC, MN=AC/2. Аналогично LK||AC, LK=AC/2.
MN||LK, MN=LK => MNKL - параллелограмм (противоположные стороны параллельны и равны).
AC=BD, NK=BD/2 => MN=NK => MNKL - ромб (смежные стороны равны).
Сумма углов треугольника равна 180°.
Следствие 1. Сумма острых углов прямоугольного треугольника равна 90°.
Следствие 2. В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.
Следствие 3. В равностороннем треугольнике каждый угол равен 60°.
Следствие 4. В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
Следствие 5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Не забудь отметить ответ, как ЛУЧШИЙ)