Площадь треугольника можно вычислить как половину произведения двух сторон на синус угла между ними:
S=\frac{1}{2}ab*sin \alphaS=21ab∗sinα
1) а=2 см, b= 3 cм, α=30°
S=\frac{1}{2}*2*3*sin30^o=3*\frac{1}{2}=\frac{3}{2}=1.5S=21∗2∗3∗sin30o=3∗21=23=1.5
ответ: SΔ=1.5 cм².
2) а=2√(2dm), b= 5√(dm), α=45°
S=\frac{1}{2}*2\sqrt{2dm} *5\sqrt{dm} *sin45^o=\sqrt{2}*\sqrt{dm}*\sqrt{dm}*5*\frac{\sqrt{2}}{2}=\frac{5\sqrt{2}\sqrt{2}}{2}dm=5dmS=21∗22dm∗5dm∗sin45o=2∗dm∗dm∗5∗22=2522dm=5dm
ответ: SΔ=5dm кв.ед.
3) а=2 м, b=√3 м, α=90°
S=\frac{1}{2}*2*\sqrt{3}*sin90^o=\sqrt{3}*1=\sqrt{3}S=21∗2∗3∗sin90o=3∗1=3
ответ: SΔ=√3 м².
4) а=0,4 см; b=0,8 см; α=60°
S=\frac{1}{2}*0,4*0,8*sin60^o=0,2*0,8*\frac{\sqrt{3}}{2}=0,1*0,8*\sqrt{3}=0,08\sqrt{3}S=21∗0,4∗0,8∗sin60o=0,2∗0,8∗23=0,1∗0,8∗3=0,083
ответ: SΔ=0,08√3 см²
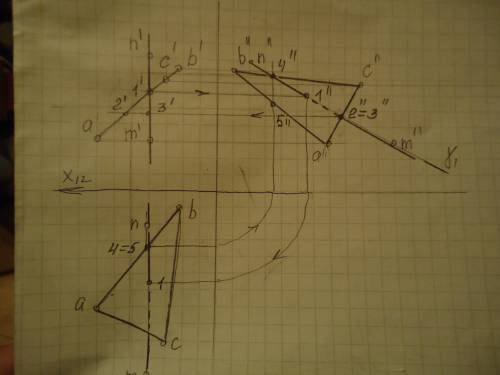
ответ: Построение точки пересечения см. на фото.
Объяснение:
Задание относится к "Начертательной геометрии".
Постройте профильные проекции прямой и треугольника.
Точка 1¹- проекция точки пересечения прямой и плоскости на виде спереди. Найдите проекцию 1¹¹ на виде слева.
Для того, чтобы определить видимость на виде слева, выберем совпадающие точки 2¹¹ и 3¹¹. Получив точки 2¹ и 3¹, видим,что треугольник к наблюдателю ближе, чем прямая. Видимость на виде слева определена.
Найдём проекцию 1 на виде сверху. На виде сверху возьмём совпадающие точки 4 и 5. Найдём их проекции на виде слева: 4¹¹ и 5¹¹. Видя, что 4¹¹, принадлежащая прямой, находится выше, чем 5¹¹ на а¹¹b¹¹, получаем, что на виде сверху в этом месте видна прямая.
Надеюсь, что смогла вам
80 см²
Объяснение:
Если в трапецию можно вписать окружность, значит, сумма оснований равна сумме боковых сторон. Если меньшая боковая сторона прямоугольной трапеции 8 см, то и высота трапеции 8 см.
Дано АВСD - трапеция, ∠А=∠В=90°, АВ=8 см, СD=12 см. Найти S.
АВ+СD=8+12=20 см, значит, АD+ВС=20 см
S=(АD+ВС):2*АВ=10*8=80 см²