. Сума кутів трикутника. Зовнішній кут трикутника
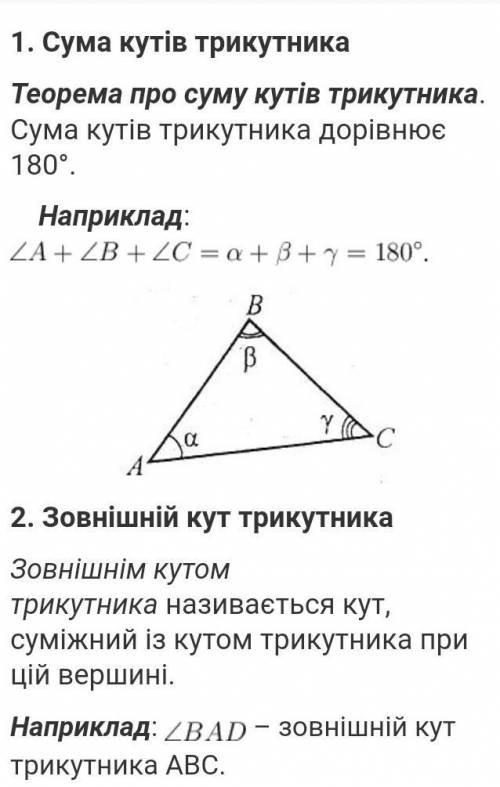
1. Сума кутів трикутника
Теорема про суму кутів трикутника. Сума кутів трикутника дорівнює 180°.
w
2. Зовнішній кут трикутника
Зовнішнім кутом трикутника називається кут, суміжний із кутом трикутника при цій вершині.
Наприклад: – зовнішній кут трикутника АВС.
Із теореми про суму кутів трикутника випливають такі висновки:
1. У будь-якого трикутника хоча б два кути є гострими.
2. Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних із ним.
Наприклад: .
3. Зовнішній кут трикутника більший за будь-який внутрішній кут, не суміжний із ним.
Наприклад: .
4. Сума гострих кутів прямокутного трикутника дорівнює 90°.
Наприклад: .
. Сума кутів трикутника. Зовнішній кут
4.42 плоскость a параллельна параллелограмму
4.45 15
Объяснение:
4.42 предположим что это не так, тогда плоскость a пересекается с плоскостью пар-ма по некоторой прямой c. так как AB и BC не параллельны одна из них (например AB, для BC аналогично) пересекает данную прямую. Так как AB и a параллельны они лежат в некоторой общей плоскости, при том b является пересечением данной плоскости и a, и эта плоскость пересекает с в той же точке что и AB, это противоречит параллельности AB и a. Значит плоскость a параллельна параллелограмму.
4.45 AC║BD иначе их точка пересечения была бы точкой пересечения α и β, а они параллельны. Значит ABCD - параллелограмм и AC = BD = 15
1.
1) Пусть дан прямоугольный тр-к АСВ с прямым углом С, катетом АС=12 см и радиусом вписанной окр-ти r=5 см.
2) Пусть катет СВ=х см. По формуле r=(2S)/P, где r=5 - радиус вписанной окр-ти, S=0,5*AC*BC=0,5*12*x=6x, а Р=АС+ВС+АВ=12+х+sqrt(144+x^2).
Получим уравнение: 5=[12x]/[12+x+sqrt(144+x^2)] => 12x=5(12+x+sqrt(144+x^2))
=> 5*sqrt(144+x^2)=7x-60 => 25(144+x^2)=49*x^2-840x+3600 => 24*x^2-840*x=0 =>
=> 2x(x-35)=0 => x=0 (не удовлетворяет условие задачи) или х=35 (см)
3) Итак, в тр-ке АВС: АС=12 см, СВ=35 см, АВ=sqrt(144+35^2)=37 см. Тогда Р=12+35+37=84 см.