Эти задачи для устного счета. Если заданы апофема и высота, то нам сразу известен радиус вписанной в основание окружности, r^2 = 10^2 - 8^2 = 6^2; r = 6;
Кроме того, нам известен косинус двугранного уголла между любой гранью и основанием, он равен 6/10 = 3/5;
Высота основания (это равносторонний треугольник) в 3 раза больше, чем r, то есть 18. Боковая сторона равна 18/(корень(3)/2) = 12*корень(3); площадь основания 12*корень(3)*18/2 = 108*корень(3);
Можно теперь честно вычислить боковую поверхность, умножая апофему на сторону основания, потом деля пополам, и результат утроить (грани три);
Но резутьтат получится такой же, как если площадь основания поделить на косинус дувугранного угла между любой гранью и основанием, то есть на 3/5.
Общая площадь будет (1 + 5/3)*108*корень(3) = 288*корень(3);
По моему, 288 не слишком похоже на 468, но это правильный ответ.
Хотите, можно и так посчитать. r = 6; значит половина боковой стороны 6*ctg(30) = 6*корень(3); сторона 12*корень(3), периметр 36*корень(3), площадь 6*36*корень(3)/2 = 108*корень(3). Опять тот же результат
Боковая грань - основание 12*корень(3), высота 10, площадь 12**корень(3)*10/2 = 60**корень(3), граней 3, всего 180*корень(3); складываем и опять получаем то же самое Хотите, еще счета расскажу? и все дадут правильный результат, а не тот, который вы хотите получить :
<А=<С=120°, <В<Д=60°
Объяснение:
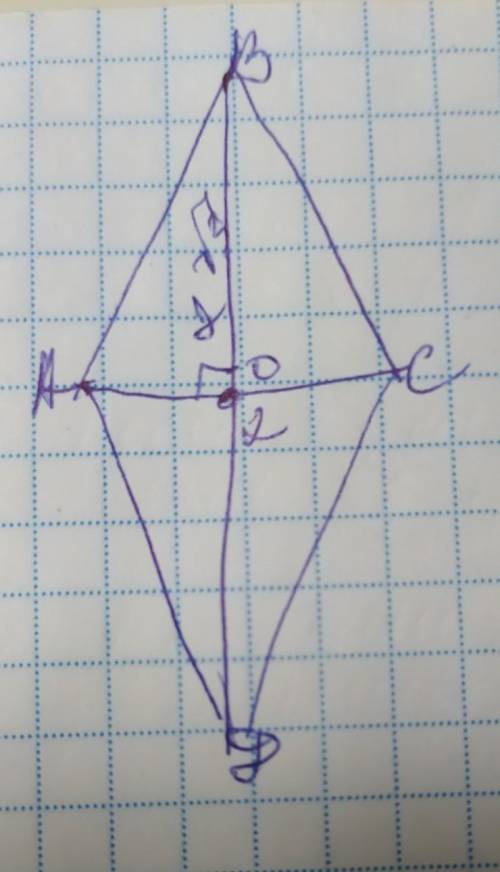
обозначим вершины ромба А В С Д с диагоналями АС и ВД а точку их пересечения О. Диагонали ромба пересекаясь делятся пополам под прямым углом, образуя 4 равных прямоугольных треугольника, а также противоположные углы ромба равны и диагонали при пересечении делят углы из которых они проведены, пополам, поэтому АО=СО=2÷2=1см, ВО=ДО=2√3÷2=√3см
Теперь найдём угол через тангенс угла АВО. Тангенс угла - это отношение противолежащего от
угла катета к прилежащему:
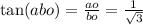
tg 1/√3=30°- это половина угла В,
Тогда <В=<Д=30×2=60°
Сумма углов ромба, прилегающие к одной стороне, составляет 180°, поэтому <А=<С=180–60=120°
обращаю внимание что 1/√3=√3/3, поскольку 1/√3 - это сокращённая дробь от √3/3. В тригонометрической таблице указано именно √3/3
Боковые стороны четырехугольника АА1В1В параллельны по условию, ⇒ АА1В1В - трапеция. Т.к. АС=СВ и СС1║АА1║ВВ1, СС1 - средняя линия трапеции и равна полусумме её оснований.
СС1=(АА1+ВВ1):2=(5+7):2=6