О - центр окружности
АВ=АС, /ОАВ=/ОАС=120:2=60 град (св-ва отрезков касательных, проведённых к окружности из одной точки)
Треуг. ОАВ - прямоугольный (ОВ - это радиус, проведённый в т.касания)
сtg/OAB=AB/OB, АВ=OB*сtg60град=9*(√3/3)=3√3
АС=АВ=3√3
Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. Данный треугольник Пифагоров и гипотенуза равна 5см.
Точка М - центр описанной окружности.
Точка О - центр вписанной окружности.
Тогда R=2,5см, то есть ВМ=2,5см.
Радиус вписанной окружности равен по формуле:
r=(AC+BC-АВ)/2 = 2/2=1см.
Итак, СН=r=1см => HB=3-1=2см.
PB=HB=2см (касательные из одной точки).
Тогда МР=2,5-2=0,5см. В прямоугольном треугольнике ОМР по Пифагору:
ОМ=√(1²+0,5²)= √1,25 ≈ 1,118 ≈ 1,12см .
ответ: расстояние между центрами окружностей равно
√1,25 ≈ 1,12 см.
Или так: по теореме Эйлера в треугольнике расстояние между центрами вписанной и описанной окружностей находится по формуле:
d² = R² - 2·R·r.
В нашем случае R = 2,5см, а r = 1cм.
тогда d = √(2,5² -2·2,5) = √(2,5·0,5) = √1,25 ≈ 1,12 см.

ответ: 10 (т.е. и вычислять ничего не нужно)))
а доказательство (аргументы для решения) может быть разным...
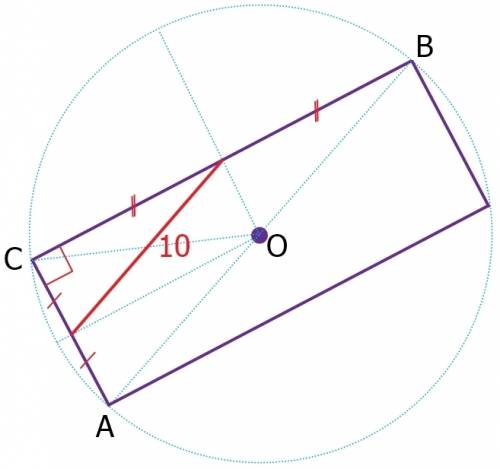
т.к. хорды по условию имеют общую точку (точку С), следовательно, ∡АСВ=90°
расстояние (которое нужно найти) называется радиусом окружности - это расстояние от центра до точки на окружности (до точки С)
известно: Прямой угол опирается на диаметр (диаметр=2*радиус).
"Расстояние между серединами" сторон треугольника - это средняя линия треугольника.
известно: Средняя линия треугольника (соединяет середины двух сторон треугольника) параллельна третьей стороне треугольника и равна ее половине. ---> диаметр=20; радиус=10...
а еще можно вспомнить: Около любого прямоугольника можно описать окружность. Радиус, перпендикулярный хорде, делит ее пополам. Диагонали прямоугольника равны.
на рисунке я провела эти радиусы и получился еще один прямоугольник (четверть большого прямоугольника), в котором диагонали равны...
АВ и АС - перпендикулярны радиусам в точке их касания.
Следовательно, соединив точку А с центром радиуса, получим два прямоугольных треугольника АОВ и АОС.
Угол ВОС делится прямой АО на два равных угла по 60°, т.к. точки В и С равноудалены от центра окружности, и АО делит этот угол пополам.
Отсюда углы ВАО = САО и равны 30° .
Радиус получившихся прямоугольников - меньший катет, лежащий против угла 30° . АО - гипотенуза этого треугольника и равна 2 катетам=2 радиусам.
АО=9*2=18 см.