Question

Синус, косинус, тангенс, котангенс. соотношения в прямоугольном треугольнике. 9 класс​

Answer 1

$cos(\beta) = \frac{8}{17}.$ Найдите площадь ΔАВС.

- - -

Дано :

ΔАВС - прямоугольный (∠С = 90°).

СВ = 8.

$cos(\beta) = \frac{8}{17}.$

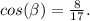
Найти :

S(ΔABC) = ?

Решение :Косинус острого угла прямоугольного треугольника - это отношение прилежащего катета к гипотенузе.

Отсюда :

$cos(\beta) = \frac{8}{17}\\\\cos(\beta) = \frac{CB}{AB}\\\\\frac{8}{17} = \frac{8}{AB}\\\\\boxed{AB = 17}$

По теореме Пифагора :

CB² + AC² = AB²

AC² = AB² - CB² = 17² - 8² = 289 - 64 = 225

АС = √АС² = √225 = 15.

Площадь прямоугольного треугольника равна половине произведения его катетов.

Отсюда :

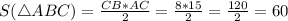$S(\triangle ABC) = \frac{CB*AC}{2} = \frac{8*15}{2} = \frac{120}{2} = 60$ (ед²).

ответ :

60 (ед²).