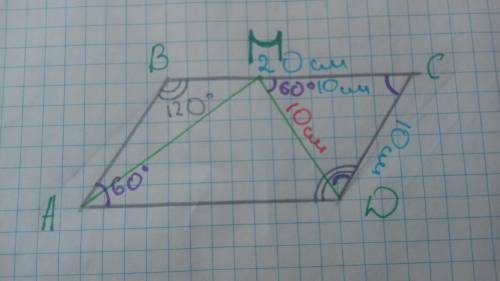
а) AB=CD=10см
BC=AD=20см
б) ABC=CDA=120 градусов
BAD=BCD=60 градусов
Объяснение:
когда мы провели биссектрису MD у нас получился равносторонний треугольник у которого все стороны одинаковые: CD=DM=MC=10см и углы равняются 60 градусам: DMC=MCD=CDM=60 градусам. теперь нам известно, что стороны CD=BA=10см по скольку эти стороны параллельные. в суме эти два угла дают 20 см. чтобы найт другую сторону параллелограмма нам надо от периметра отнять 20 см и поделить на 2: (60-20):2=20 - сторона BC (AD) .углы MCD=BAD=60 градусам. чтобы найти углы ABC и BCD мы от 180 градусов отнимаем угол ABC (BCD) (потому что углы на одной стороне параллелограмма равны 180 градусам): ABC (BCD)= 180-60=120 градусов
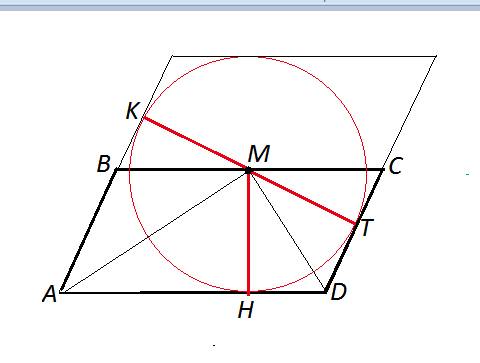
Углы ВАМ и ВСМ опираются на диаметр окружности и потому - прямые и равны 90°.
Точкой пересечения хорды и диаметра радиус ВО делится на равные части. Поэтому в треугольнике ВАС угол ВАС равен углу ВСА и равен 30 градусам.
Отсюда угол АВС равен 120°, а угол АМС =60°.
Дуги ВСМ и ВАМ равны по 180°.
Дуга ВАС равна 120°, так как центральный угол, опирающийся на нее, равен 120° градусов, а вписанный АМС=60°.
Дуга АВМ вписанного угла АВС=120*2=240°.
Итак:
Углы
ВАМ и ВСМ=90°
АВС=120°
АМС=60°
Дуги
АВС=240°
ВАМ=АСМ=180°
АМС=120°