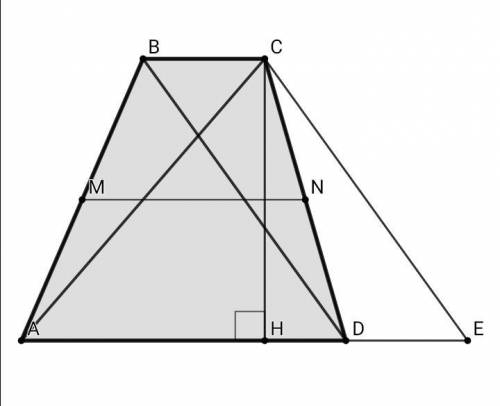
Выведу обобщённую формулу для подобных задач про трапецию с известными диагоналями AC = x, BD = y, и суммой оснований BC + AD = m
Проведём из вершинны С прямую СЕ, параллельную BD, тогда BC || DE, CE || BD ⇒ BCED - параллелограми, ВС = DE, CE = BD = y
S (abcd) = (BC + AD)•CH/2 = (DE + AD)•CH/2 = AE•CH/2 = S (ace)
Площадь трапеции ABCD равна площади треугольника ACE
Найдём плошадь ΔАСЕ по формуле Герона: АС = х, CE = y, AE = m
Площадь трапеции с диагоналями х и у и суммой оснований равной m:S = √( p • (p - x) • (p - y) • (p - m) ) , где р = (х + y + m)/2Средняя линия трапеции: MN = (BC + AD)/2 = 5 ⇒ m = 10, x = 9, у = 17
S (abcd) = √(18•(18 - 9)(18 - 17)(18 - 10)) = √(18•9•1•8) = 36ответ: 36
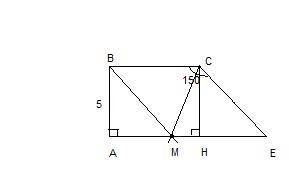
12
Объяснение:BD - наибольшая диагональ = 12√3.
<A = 120.
1) Посколько диагонали ромба одновременно перпедикулярны (т.е. создают 4 угла по 90°) и являются биссектрисами углов, то меньшая биссектриса AC разбивает <A на 60°.
Из треугольника ABO, нам известно, что <O = 90°. Не сложно найти тогда и <B:
2) DB = 2OB, посколько диагонали ромба точкой сечения делятся пополам, т.е OB = 6√3
Из треугольника ABO найдём сторону AO, лично мне будет удобно использовать теорему синусов, кто-то может использовать тригонометрические соотношения углов, как вам удобно. Итак, имеем:
3) AC = 2AO, посколько диагонали ромба точкой сечения делятся пополам, т.е: