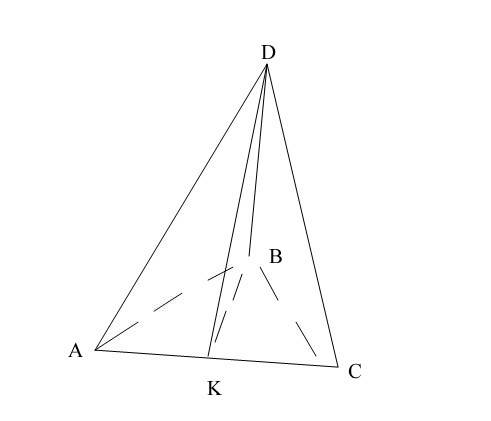
Дана треугольная пирамида ABCD, в основании которой равнобедренный треугольник АВС (АВ=ВС=5, АС=6).
Боковые грани пирамиды, содержащие стороны АВ и ВС, перпендикулярны основание, т.е. DB - высота пирамиды.
Проведем высоту (медиану и бисс-у) ВК треугольника АВС.
Рассмотрим треугольник АКВ -прямоугольный.
АК=АС/2=3, АВ=5
ВК^2 = AB^2- AK^2
BK = 4
Рассмотрим треугольник DBK - прямоугольный.
Угол BKD=60 гр, следовательно, угол BDK=30 гр.
Катет, лежащий напротив угла 30 гр, равен половине гипотенузы.
BK=1/2DK
DK=8
DB^2 = DK^2 - BK^2
DB = корень из 48 = 4 корня из 3
Один из углов № 1=60. Идем сверху вниз.
Смежный с данным вверху угол 2 = 180-60=120.
Под первой параллельной прямой углы 3 и 4 как вертикальные равны 60 и 120.
Переходим ко второй параллельной.
Слева угол 5=120, как Соответственный углу 2 или односторонний с углом 3. Их сумма равна 180.
Справа угол 6=60, как смежный с углом 5, как соответственный углу 1=60, или как односторонний с углом 4, сумма которых равна 180.
Внизу второй параллельной слева угол 7=60, как соответственный углу 3, как внешний накрест лежащий углу 1.
И последний угол 8 =120. как соответственный углу 4, или смежный с углом 6.