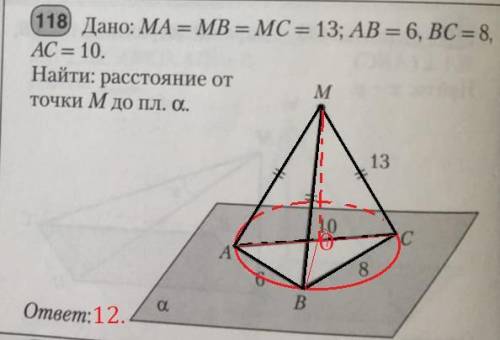
Точка M, равноудалена от вершин треугольника ABC, поэтому она лежит на перпендикуляре к (ABC), который восстановлен из центра (O) описанной около ΔABC окружности. Треугольник со сторонами 6, 8, 10 является египетским (10²=6²+8²), поэтому ∠B=90°, а значит центр описанной лежит на середине AC. И её радиус равен AC:2=10:2=5.
Как было сказано ранее MO⊥(ABC).
Рассмотри прямоугольный ΔAOM (∠O=90°): AO=5; AM=13. Найдём второй катет MO (расстояние от M до α) по теореме Пифагора (хотя тут опять Пифагорова тройка 5, 12, 13).
MO=√(13²-5²) = √((13+5)(13-5)) = √(18·8) = √(3²·4²) = 12
ответ: 12.
110°, 35°, 35°.
Объяснение:
Внешний угол является смежным с внутренним и, значит, в сумме с ним равен 180°. => внутренний угол равен 180-70 = 110°.
Это тупой угол, он является единственным в треугольнике, значит два других - равные углы при основании по 35°. (в сумме дают внешний угол, не смежный с ними (свойство).