тут площадь ромба находится через диагонали.
Объяснение:
нам сейчас известна только одна диагональ АС =4(ОС*2), а чтобы найти площадь нужно знать две(диагонали). через теорему пифагора мы найдем вторую диаглналь. с^2=a^2+b^2, b^2=c^2-a^2, b^2=c^2(гипотенуза, в нашем случае это ВС равное 5)-a^2(это ОС равное 2) то есть в^2= 25(это 5 в квадрате) - 4(2 в квадрете) = 21(так и записывай в= корень из 21), вторая диагональ= 2*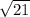
= корень(4*21)=корень(84). теперь чтобы найти площадь нужно (д1*д2)/2. получается (4*корень(84))/2. запишешь в форме дроби, ото 4 и 2 можно сократить, останется 2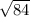
Середина диаметра центр окружности О((-4+2)/2;(7-1)/2); О(-1;3), длина диаметра равна √((2+4)²+(-1-7)²)=√(36+64)=10, радиус - половина диаметра. и он равен 10/2=5.
Уравнение окружности (х-(-1))²+(у-3)²=5²
(х+1)²+(у-3)²=25