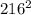
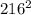
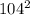
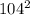
AK = CM
Объяснение:
Имеем углы KAB и MCB. Для начала нужно доказать что эти углы равны, а если эти углы будут равны, то и стороны этих углов тоже будут равны. Первое свойство равнобедренного треугольника гласит: углы при основании равнобедренного треугольника равны. Проведём медиану BD, которая будет делить данный треугольник на равные части. Т.к. углы BAD и BCD равны, то углы KAB и BAD, будут вертикальные, а значит равны. Углы MCB и BCD тоже будут вертикальные, а значит тоже равны между собой. А т.к. углы при основании равны и оба из них имеют равные прилежащие углы, то и углы KAB и MCB, тоже равны!
Решение
Первый Проведём через точку M прямую, параллельную CK, которая пересечет AB в точке D (рис. 2). По теореме Фалеса BD = KD. По теореме о пропорциональных отрезках PM = KD = ½ BK.
Второй Пусть T – середина отрезка CK (рис. 1). MT – средняя линия треугольника CBK, следовательно, MT || BK и BK = 2MT. Треугольники KAP и TMP, очевидно, подобны, поэтому MP = MT = ½ BK.
Объяснение: