Сначала немного рассуждений.
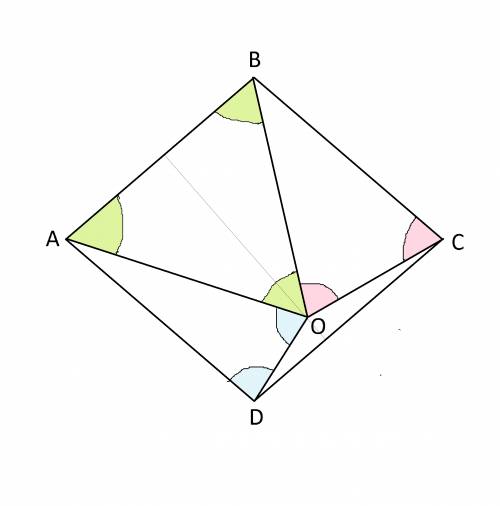
На стороне АВ вершиной внутрь ромба построен равносторонний треугольник.
Стороны этого треугольника равны сторонам ромба ( АВ - сторона ромба, у ромба все стороны равны, у равностороннего треугольника - тоже), а острый угол ромба больше 60°, иначе сторона АО построенного треугольника АОВ должна совпасть со стороной АD ромба.
Углы равностороннего треугольника равны 60°.
Сумма углов ромба, прилегающих к одной стороне, равна 180°.
Следовательно
∠DАО+∠СВО=180°-(ОАВ+ОВА)=180° -60°*2=60°
Рассмотрим треугольники DАО и СВО.
Они - равнобедренные, так как АВ=АD=АО=BO=ВС по условию задачи - стороны треугольника АОВ равны сторонам ромба и равны АВ.
Сумма всех углов ᐃ DАО и ᐃ СВО равна 180°*2=360°.
Углы в каждом из них при основаниях равны.
Сумма углов при основании ᐃ АОD+ cумма углов при основании ᐃ ВОС=
(360°- (∠DАО+∠СВО)=360°-60°)=300°
Сумма ∠DОА+∠ СОВ=300°:2=150°
Сумма всех углов при точке О равна 360°
Угол СОD=360-(∠АОD+ВОD)- АОВ=360°-150°-60°=150°
сначала найдем разность прогрессии (d):
d = a2 - a1 = -24 - (-16) = - 8
а теперь по формуле n-ого члена найдем 61 член прогрессии:
an = a1 + (n-1)d
a61 = (-16) + (61-1) * (-8)
a61 = (-16) + 60 * (-8)
a61 = -(16) + (-480)
a61 = - 496
ответ: a61 = - 496