
Два угла треугольника равны 40° и 52°. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов.
- - -
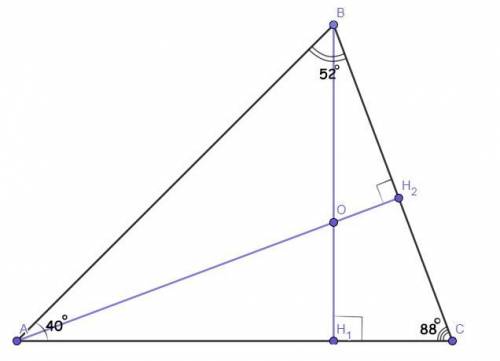
Дано :ΔАВС.
∠А = 40°.
∠В = 52°.
ВН₁ и АН₂ - высоты.
Точка О - ортоцентр (точка пересечения высот).
Найти :∠АОВ = ? (или ∠Н₁ОН₂, не важно, так как они равны как вертикальные).
Решение :Немного о расположении ортоцентра О :
Для начала найдём ∠С.
По теореме о сумме углов треугольника -
∠А + ∠В + ∠С = 180°
∠С = 180° - ∠А - ∠В
∠С = 180° - 40° - 52°
∠С = 88°.
Так как все углы ΔАВС - острые, то ортоцентр О лежит внутри ΔАВС.
- - -
Рассмотрим ΔСВН₁ - прямоугольный (так как ∠ВН₁С = 90° по определению высоты треугольника).
Сумма острых углов прямоугольного треугольника равна 90°.Тогда -
∠Н₁СВ + ∠Н₁ВС = 90°
∠Н₁ВС = 90° - ∠Н₁СВ
∠Н₁ВС = 90° - ∠Н₁СВ
∠Н₁ВС = 90° - 88°
∠Н₁ВС = 2°.
Теперь рассмотрим ΔОВН₂ - прямоугольный (так как ∠ОН₂В = 90°).
По выше сказанному -
∠ВОН₂ + ∠ОВН₂ = 90°
∠ВОН₂ = 90° - ∠ОВН₂
∠ВОН₂ = 90° - 2°
∠ВОН₂ = 88°.
- - -
∠ВОН₂ и ∠АОВ - смежные.
Сумма смежных углов равна 180°.Следовательно -
∠ВОН₂ + ∠АОВ = 180°
∠АОВ = 180° - ∠ВОН₂
∠АОВ = 180° - 88°
∠АОВ = 92°.
ответ :92°.
1)Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник будет являться параллелограммом.
Объяснение:
Рассмотрим четырехугольник ABCD. Пусть в нем стороны AB и СD параллельны. И пусть AB=CD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD.
Эти треугольники равны между собой по двум сторонам и углу между ними (BD - общая сторона, AB = CD по условию, угол1 = угол2 как накрест лежащие углы при секущей BD параллельных прямых AB и CD.), а следовательно угол3 = угол4.
А эти углы будут являться накрест лежащими при пересечении прямых BC и AD секущей BD. Из этого следует что BC и AD параллельны между собой. Имеем, что в четырехугольнике ABCD противоположные стороны попарно параллельны, и, значит, четырехугольник ABCD является параллелограммом.
2)Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник будет параллелограммом.
Доказательство:
Рассмотрим четырехугольник ABCD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD.
Эти два треугольника буду равны между собой по трем сторонам (BD - общая сторона, AB = CD и BC = AD по условию). Из этого можно сделать вывод, что угол1 = угол2. Отсюда следует, что AB параллельна CD. А так как AB = CD и AB параллельна CD, то по первому признаку параллелограмма, четырехугольник ABCD будет являться параллелограммом.
3)Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник будет являться параллелограммом.
Рассмотрим четырехугольник ABCD. Проведем в нем две диагонали AC и BD, которые будут пересекаться в точке О и делятся этой точкой пополам.
Треугольники AOB и COD будут равны между собой, по первому признаку равенства треугольников. (AO = OC, BO = OD по условию, угол AOB = угол COD как вертикальные углы.) Следовательно, AB = CD и угол1 = угол 2. Из равенства углов 1 и 2 имеем, что AB параллельна CD. Тогда имеем, что в четырехугольнике ABCD стороны AB равны CD и параллельны, и по первому признаку параллелограмма четырехугольник ABCD будет являться параллелограммом.
Подробнее - на -
●2●
нет, это не параллелограм, т.к. диагонали параллелограмма точкой пересечения делятся пополам, а на рисунке АО > ОС.
Нет,так как диоганали точкой делятся пополам у параллелограмма, а тут 7 и 6.
●ответ:● а и б не является параллелограмом, а в и г да
●Объяснение:●
Т.к углы пар. являются паралельный друг к другу.
●3●
Решение на фото