Если вас еще интересует решение этой задачи, то здесь не так уж и сложно.
Нужно воспользоваться формулами для нахождения диагоналей параллелограмма через его стороны.
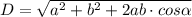
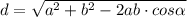
D - большая диагональ, d - малая диагональ.
Подставляем длины сторон и диагоналей и находим угол 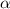
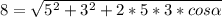
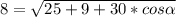
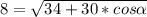
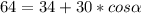
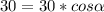
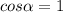

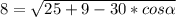

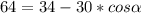
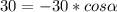
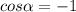
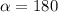
Как видим, углов между сторонами 5 и 3, при которых одна из диагоналей могла бы равняться 8, и при которых сещуствовал бы параллелограмм, нет.
Вот и вывод: диагональ параллелограмма не может равняться 8 при сторонах 5 и 3.

Так как длины сторон четырёхугольника пропорциональны числам 2 : 3 : 4 : 5, то пусть их длины равны соответственно 2х, 3х, 4х, 5х (х — коэффициент пропорциональности).
Периметр — это сумма длин всех сторон.Следовательно :
2х + 3х + 4х + 5х = 56 см
14х = 56 см
х = 56 см : 14
х = 4 см.
2х = 2*4 см = 8 см.
2х = 2*4 см = 8 см.3х = 3*4 см = 12 см.
2х = 2*4 см = 8 см.3х = 3*4 см = 12 см.4х = 4*4 см = 16 см.
2х = 2*4 см = 8 см.3х = 3*4 см = 12 см.4х = 4*4 см = 16 см.5х = 5*4 см = 20 см.
ответ : 8 см, 12 см, 16 см, 20 см.