1. Описать окружность можно только около равнобедренной трапеции, а у нее углы при основании равны, а углы, прилежащие к боковой стороне составляют в сумме 180, поэтому углы будут 49°; 180°-49°=131°. ответ 49°; 131°; 131°.
2. Т.к. ОА и ОВ - радиусы, проведенные в точки касания, а СА=СВ по свойству отрезков касательных. проведенных из одной точки, то прямоугольные треугольники АОС и ВОС равны по гипотенузе и катету. (∠А=∠В=90°), значит, ∠АОС=∠ВОС⇒=90°-0.5∠АСО, тогда ∠АОВ=180°-83°=97°
3. Периметр равен 36, значит, сторона 36/4=9, высота ромба равна частному от деления площади на сторону, то есть 54/9=6
4. tg∠B=АС/ВС=7/2=3.5
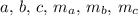- длины сторон и медиан треугольника ABC, 
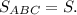Воспользовавшись формулу 
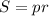и то, что 
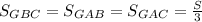, получаем, что нужно доказать неравенство.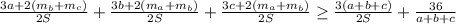
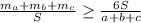
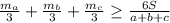
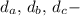расстояния от точки G к сторонам a, b, c треугольника АВС. Очевидно, что 
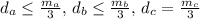Также имеем
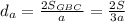. Аналогично,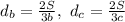 
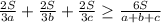, которое равносильна неравенству, что выражает отношение между средним арифметическим и средним гармоническим 3 положительных чисел: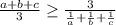
AOC=12
BOC=12×3=36
AOB=36+12=48
AOB=48