Наименьший угол треугольника равен ≈ 20,7°.
Объяснение:
Наименьший угол лежит против наименьшей стороны треугольника, то есть против стороны, равной 8 ед.
Находим площадь треугольника АВС по Герону:
S = √(p(p-a)(p-b)(p-c)), где р - полупериметр, a,b,c - стороны.
p = (12+18+8)/2 = 19 ед.
S = √(19·7·1·11) = √1463 ≈ 38,25 ед.
С другой стороны, по формуле площади треугольника:
S = (1/2)·a·b·Sinα. В нашем случае:
38,25 = (1/2)·12·18·Sinα =>
Sinα =(38,23·2)/(12·18) ≈ 76,5/216 = 0,354.
α = arcsin0,354 ≈ 20,73°. (по калькулятору или таблице).
Или так:
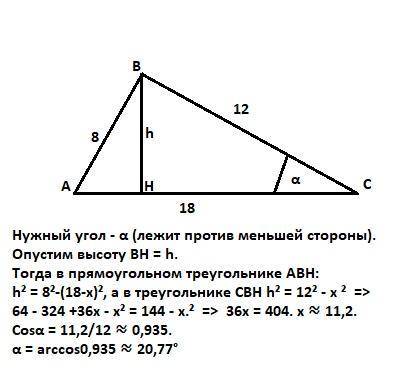
Нужный угол - α (лежит против меньшей стороны).
Опустим высоту BH = h.
Тогда в прямоугольном треугольнике АВН:
h² = 8²-(18-x)², а в треугольнике СВН h² = 12² - х ² =>
64 - 324 +36x - x² = 144 - x.² => 36х = 404. х ≈ 11,2.
Cosα = 11,2/12 ≈ 0,935.
α = arccos0,935 ≈ 20,77° (по калькулятору).
9.рассмотрим треугольники ROP и OPS: углы ROP=SOP(по рисунку), OP-общая сторона, углы RPO=OPS(по рисунку) следует треугольник равны по 2 признаку
10. рассмотрим треугольник oad и ocd: угл О-общий, oc=od по рисунку, углы oda=ocb по рисунку, следует треугольники равны по 1 признаку
11. рассмотрим треугольники MPK и KPN: KP-(ОБЩАЯ СТОРОНА), KM=KN(ПО РИСУНКУ), УГЛЫ MKP=PKM (по рисунку), следует треугольник равен по 1 признаку
12. рассмотрим треугольники abc и cad, ad=bc по рисунку, cd=ab по рисунку, ac-общая сторона, следует треугольник равны по 3 признаку
13. рассмотрим треугольники adc и cdb, cd- общая сторона, углы acd=dcb по рисунку, углы adc=bdc по рисунку, следует треугольники равны по 2 признаку
14.рассмотрим треугольники rpq и rqs, rg- общая сторона, углы prq=rqs по рисунку, углы pqr=qrs по рисунку, следует треугольник равны по 2 признаку.
15. рассмотрим треугольники abd и dbc, db-общая, углы adb=dbc по рисунку, углы cdb=abd, следует треугольники равны по 2 признаку.
16. рассмотрим треугольники ktm и tps, kt=tp по рисунку, mt=ts по рисунку, углы ktm=stp ( т.к вертикальные углы) следует треугольники равны по 1 признаку