а) Треугольник АВС равнобедренный с боковыми сторонами АВ=ВС. б) В треугольнике АВС: ∠А = ∠С = 70°, ∠В = 40°.
Объяснение:
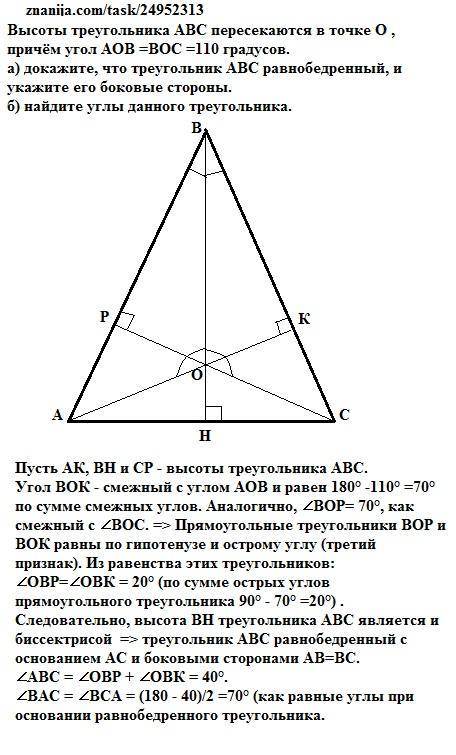
Пусть АК, ВН и СР - высоты треугольника АВС.
Угол ВОК - смежный с углом АОВ и равен 180° -110° =70°по сумме смежных углов. Аналогично, ∠ВОР= 70°, как смежный с ∠ВОС. => Прямоугольные треугольники ВОP и ВОК равны по гипотенузе и острому углу (третий признак). Из равенства этих треугольников:
∠ОВР=∠ОВК = 20° (по сумме острых углов прямоугольного треугольника 90° - 70° =20°) .
Следовательно, высота ВН треугольника АВС является и биссектрисой => треугольник АВС равнобедренный с основанием АС и боковыми сторонами АВ=ВС. Что и требовалось доказать.
∠АВС = ∠ОВР + ∠ОВК = 40°.
∠ВАС = ∠ВСА = (180 - 40)/2 =70° (как равные углы при основании равнобедренного треугольника.
2. 42°, 138°
3. 87 и 106 градусов
4. 336, 336, 12, 12
Объяснение:
2. (180° - 96°) : 2 = 42° - меньший угол
42° + 96° = 138° - больший
3. Решим данную задачу при уравнения.
Пусть один из смежных углов х градусов, тогда второй из смежных углов (х + 32) градусов. Нам известно, что сумма градусных мер смежных углов равна 180 градусов. Составляем уравнение:
х + х + 32 = 180;
х + х = 148;
х * (1 + 1) = 148;
х * 2 = 148 (для того, чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель);
х = 148 : 2;
х = 74 градусов — один из смежных углов;
74 + 32 = 106 градусов — второй из смежных углов.
4. При пересечении 2 прямых образуется 4 угла, углы ровны попарно
360-(12+12)=336 градуса - это два тупых угла
336:2=168 градуса - один тупой угол