120,120,60,60
Объяснение:
Это второй рисунок
Касательная NM перпендикулярна радиусу ON. ONM - прямоугольный треугольник. Катет против угла 30° равен половине гипотенузы. ON=OM/2 => ∠NMO=30°. Касательные из одной точки составляют равные углы с прямой, проходящей через эту точку и центр окружности.
∠NMK=2∠NMO =30°*2 =60°
Это четвёртый рисунок
∠BAM найден в задаче (3) =30°. Отрезки касательных из одной точки равны, AM=BM, △AMB - равнобедренный, ∠BAM=∠ABM.
∠AMB=180°-2∠BAM =180°-30°*2 =120°
Это первый рисунок Касательная KL перпендикулярна радиусу OK. OKL - прямоугольный треугольник. Катет против угла 60° равен другому катету, умноженному на √3.
KL=OK√3 =6√3
Это третий рисунок Треугольник OAB - равносторонний (OA=OB - радиусы), ∠OAB=60°. Касательная AC перпендикулярна радиусу OA, ∠OAС=90°.
∠BAC=∠OAC-∠OAB =90°-60° =30°
Это пятый рисунок Касательная MN перпендикулярна радиусу OM. OMN - египетский треугольник (3:4:5) cо множителем 3 (OM=4*3; ON=5*3). MN=3*3=9
а) Координаты середины отрезка равны полусуммам соответствующих координат его концов.
А (2; -1; 0), В (-4; 2; 2)
Обозначим середину отрезка АВ буковой К
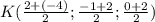
К (-1; 0,5; 1)
б) Нужно найти координаты точки С, если точка В является серединой отрезка АС. Координаты точек А и В известны. Координаты точки С обозначим (x; y; z). И используем формулу для нахождения координат середины отрезка. Находим координаты середины отрезка АС.
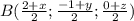
Координаты точки В известны. Приравняем их и получим три уравнения, решая которые найдем координаты точки С.
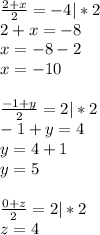
C (-10; 5; 4)
в) Длина отрезка можно вычислить так: квадратный корень из суммы квадратов разностей соответствующих координат концов отрезка.
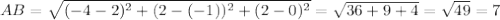
АВ=7
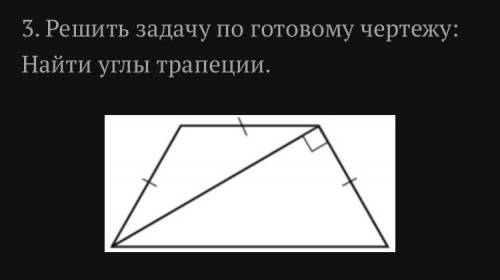
ответ: 60*, 120*, 120* 60*.
Объяснение:
Сумма углов в четырехугольнике равна (n-2)*180=(4-2)*180*=2*180*=360*.
Обозначим трапецию через ABCD, где AB=BC=СD (по условию).
∠BAC=∠BCA, т.к. треугольник ABC - равнобедренный.
∠CAD=∠ACB, как накрест лежащие при BC║AD и секущей CD.
Обозначим ∠BAC=∠BCA=CAD через х. Тогда ∠ADC=2x, так как АС является биссектрисой угла BAD.
Cосотавим уравнение:
2х+2х+90*+х+90*+х=360*.
6х=360*-180*;
6х=180*;
х=30*;
Тогда ∠BAD=2*30*=60*;
∠ABC=90*+30*=120*;
∠BCD=∠ABC=120*;
∠CDA=∠BAD=60*.
Проверим:
60*+120*+120*+60*=360*.