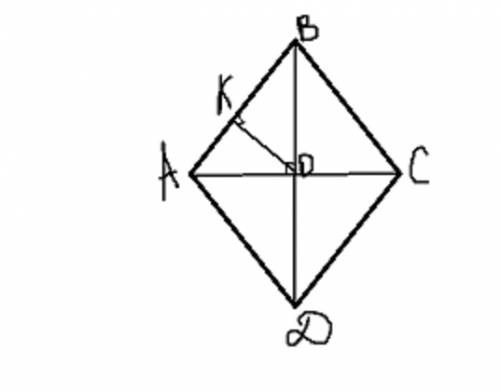
1) Рассмотрим треугольник АОВ прямоугольный
(т.к. по свойству ромба диагонали пересекаются под прямым углом)
Высота, выходящая из прямого угла треугольника, делит этот треугольник на подобные треугольники!
следует треугольник ОКВ подобен АОВ! следует КВ/OB=OK/OA
(OB=OД=8),
мы можем найти KB из треугольника OKB (по т.Пифагора)
KB"2=64-48=16; KB=4
(подставим все значения и найдём OA):
4/8=4 корня из 3/OA
ОА = 4 корня из 3*8/4=8 корней из 3
AC=2AO=16 корням из 3
из треугольника АОВ найдём AB = корень из (64+192)=корень из 256 = 16
Прямая, содержащая высоту равнобедренного треугольника, является и его медианой, следовательно, она является срединным перпендикуляром к хорде, и поэтому проходит через центр окружности. Обозначим исходный треугольник через ABC (AC - основание), через M - середину AC, через O - центр окружности. В прямоугольном треугольнике BOC высота CM является средним пропорциональным проекций катетов на гипотенузу, поэтому |MO| = |MC|2/|BM| = 16/3. Из прямоугольного треугольника OCM по теореме Пифагора получаем, что |OC|2 = |OM|2+|MC|2 = (20/3)2. или =
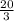
1) Если треугольник прямоугольный, то:
Х+8Х+90=180
9Х=90
Х=10 град один остр угол
Х*8=80 град второй остр угол
2) Если угол при вершине =100 гр, то находим угол вершины:
180-100=80гр
Теперь находим углы при основании:
(180-80):2=50гр каждый угол при основании.
ответ: 80гр, 50гр, 50гр.
3) Вычисляем внутренние углы (которые являются смежными с внешними углами):
180-125=55гр
180-145=35гр
определяем, является ли третий угол прямым:
180-(55+35)=90гр
Угол 90гр - прямой, следовательно тр-к АВС - прямоугольный