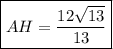
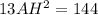
Объяснение:
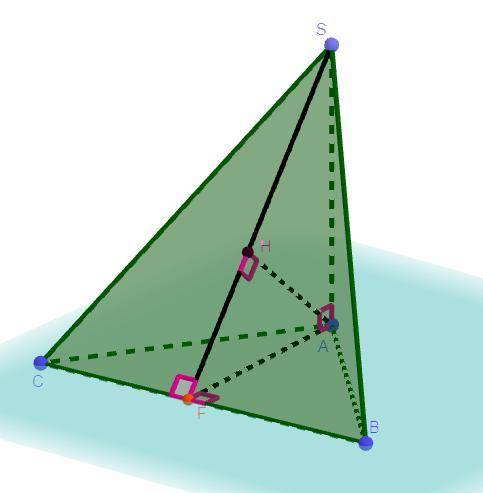
Дано: Пирамида ABCS, AS ⊥ ABC, AB = AC = BC = 4, AS = 12, AH ⊥ SBC
Найти: AH - ?
Решение: Проведем высоту в треугольнике ΔABC к стороне BC в точку F, так как по условию треугольник ΔABC - равносторонний, то по свойствам равностороннего треугольника его высота является биссектрисой и медианой, следовательно BF = CF. Треугольник ΔCAS = ΔBAS(AS ⊥ ABC по условию, поэтому треугольник ΔCAS и ΔBAS - прямоугольные) по двум катетам, так как AS - общая и AC = BC по условию, из равенства треугольников следует, что SC = SB, тогда треугольник ΔSCB - равнобедренный. Проведем отрезок SF, так как треугольник ΔSCB - равнобедренный(SC = SB, следовательно BC - основание), то по теореме медиана опущенная на высоту является биссектрисой и высотой, тогда SF ⊥ BC.
Так как по условию AH ⊥ SBC, то AH перпендикулярно любой прямой лежащей в плоскости SBC, то AH ⊥ SF (SF ∈ SBC), так как SF - гипотенуза прямоугольного треугольника ΔSAF (по условию AS ⊥ ABC) и так как SF - гипотенуза прямоугольного треугольника ΔSAF (по условию AS ⊥ ABC), то отрезок AH - высота прямоугольного треугольника ΔSAF проведенная к гипотенузе.
Рассмотрим прямоугольный треугольник ΔCAF(AF ⊥ BC по построению). Так как треугольник ΔABC - правильный по условию, то по свойствам правильного треугольника все его углы 60°, следовательно ∠BCA = 60°.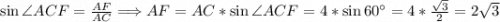 
.
Рассмотрим треугольник ΔSAF, по теореме Пифагора: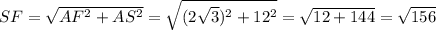 
.
По формуле площади прямоугольного треугольника: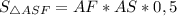
, с другой стороны 
AS * AF * 0,5 = AH * SF * 0,5|:0,5SF
.
.
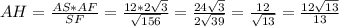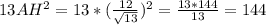Пусть B - начало координат
Ось X - BC
Ось Y - перпендикулярно X в направлении A
Ось Z - перпендикулярно ABC в направлении S
Координаты точек
С ( 2;0;0)
S ( 1; √3;4)
A ( 1; √3;0)
Уравнение плоскости SBC ( проходит через начало координат )
ax + by + cz = 0
Подставляем координаты точек S C
2a=0
a+√3b + 4c =0
Откуда a=0
Пусть b = 4/(√3) тогда с = -1
Уравнение плоскости SBC
4y/√3 - z = 0
Нормальное уравнение плоскости
k= √(16/3+1) = √(19/3)
4y/√19 - √3z/√19 =0
Подставляем координаты точки A в нормальное уравнение для нахождения расстояния от точки А до плоскости SBC ( оно же длина высоты AH )
4 * √3 / √19
По условию просят 19 * (4√3/√19 ) ^2 = 48
1 d
2 c
3 e
4 a
5 b
Объяснение:
нет, ничего сложного