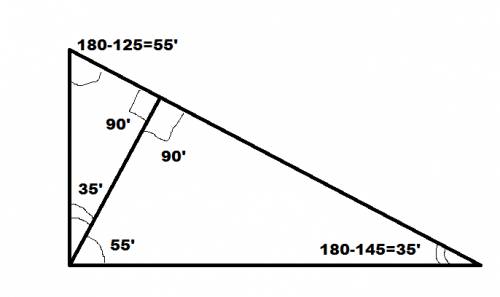
На гипотенузе при высоте каждый угол равен 90'
Так как треугольник прямоугольный, можно сказать, что, если разделить его прямой угол на две части, одна из которых будет равна 55, то вторая будет равна 35 градусам.
У нас получилось два маленьких прямоугольных треугольника в одном большом. Сумма углов любого треугольника равна 180 градусов, следовательно, третий угол в маленьком нижнем треугольнике на картинке будет равен 180-(55+90)=35 градусов.
Острые углы — это все углы меньше 90 градусов.
высоту к стороне длины 5 обозначим h, расстояние от основания этой высоты до вершины, общей со стороной длины 4 - обозначим х. Дальше сплошной Пифагор.
x^2 + h^2 = 4^2 = 16;
(5 - x)^2 + h^2 = 17;
25 - 10*x + x^2 + h^2 = 17;
25 - 10*x + 16 = 17; x = 2,4;
h = 3,2 (можно подставить в первое выражение и сосчитать, а можно увидеть, что треугольник со сторонами 2,4; h; 4; подобен треугольнику со сторонами 3; 4; 5; коэффициент пропорциональности 4/5)
Площадь (1/2)*5*3,2 = 8
По формуле Герона тоже можно вычислить, вот я бы и предложил советчику самому и сосчитать : Хотя ответ, само собой, получится такой же.
Кстати... давно хотел. обозначая стороны a,b,c, h - высота к с, х - кусок с между b и h, имеем
x^2 + h^2 = b^2;
(c - x)^2 + h^2 = a^2;
c^2 - 2*c*x + x^2 + h^2 = a^2;
x = (c^2 + b^2 - a^2)/(2*c);
h = корень(b^2 - (c^2 + b^2 - a^2)^2/(2*c)^2));
Остюда
S = c*h/2 = (1/2)*корень(с^2*b^2 - ((c^2 + b^2 - a^2)/2)^2);
Я намеренно не буду приводить эту формулу к Героновскому виду, хотя это довольно просто. Громоздко, но - несложно. Важно, что это выражение СОВЕРШЕННО РАВНОСИЛЬНО формуле Герона, а для конкректных расчетов проще - к примеру, для нашего треугольника сразу выходит
1/2*корень(16*25 - 12^2) = 8;
а вот пример отсюда
там стороны 10, 2*корень(10) и 2*корень(17).
Я по формуле Герона тупо считал час, не меньше. А по моей формулке (совершенно равносильной) это проще, чем 2х2
S = корень(4*17*4*10 - (4^2))/2 = 2*корень(170-1) = 26; почти устная задача :))