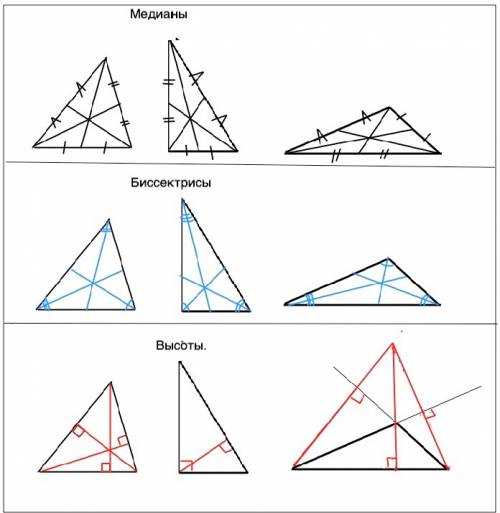
Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.
Биссектрисы треугольника пересекаются в одной точке, расстояние от которой до сторон треугольника одинаково и является центром вписанной окружности.
Высоты треугольника пересекаются в одной точке. Точка пересечения высот остроугольного треугольника находится внутри него. Точка пересечения высот прямоугольного треугольника - вершина прямого угла.
Высоты тупоугольного треугольника, проведенные из вершин его острых углов, проходят вне его и пересекают продолжения сторон. Точка пересечения высот тупоугольного треугольника находится вне треугольника.
Рассмотрим сечение ЦИЛИНДРА Это прямоугольный РАВНОБЕДРЕННЫЙ треуголльник ABC (так как углы равны по 45 град. ) т.е AC=BC .По теореме Пифагора найдем эти стороны . оставим уравнение Х^2(в квадрате)+ Х^2(в квадрате)=64 ИЗ этого следует
2Х^2(в квадрате)=64 , Х^2(в квадрате)=32 , Х=32(из под коря )=4*3(из под корня )
1 А так так ВС-это и есть высота . то BC=4*3(из под корня )
2 а AC=d(диаметру) и = 4*3(из под корня ). А r(радиус )=2/d . И из этого следует
AC=4*3(из под корня)/2= 2*3(из под корня)-ЭТО РАДИУС
ответ высота BC=4*3(из под корня ), а ралиус (r)=2*3(из под корня)
Объяснение:
АВ=Cтак как стороны квадрата равны.
Стороны квадрата попарно параллельны, тогда АВ//CD и AD//CB.
Угол ВАС=угол DCA так как накрест-лежащие при параллельных прямых АВ и CD и секущей АС.
АК=МС по условию.
Исходя из доказанных равенств: ∆АВК=∆DCM по двум сторонам и углу между ними.
Следовательно КВ=MD как соответственные стороны равных треугольников.
АD=CB так как стороны квадрата равны.
Угол DAC=угол ВСА как накрест-лежащие углы при параллельных прямых AD u BC и секущей АС.
АК=МС по условию
Исходя из доказанных равенств: ∆DAK=∆ВСМ по двум сторонам и углу между ними.
Тогда KD=MB как соответственные стороны равных треугольников.
Диагонали квадрата являются биссектрисами его углов.
Следовательно: угол DCM=угол ВСМ.
DC=BC так как это стороны квадрата.
МС – общая сторона.
Тогда ∆DCM=∆BCM.
Следовательно DM=BM как соответственные стороны равных треугольников.
Получим:
DM=BK
|| => DM=BK=BM=DK.
BM=DK
Следовательно четырехугольник BMDК – ромб, так как это четырехугольник у которого все стороны равны.