При пересечении двух прямых образуются четыре угла.
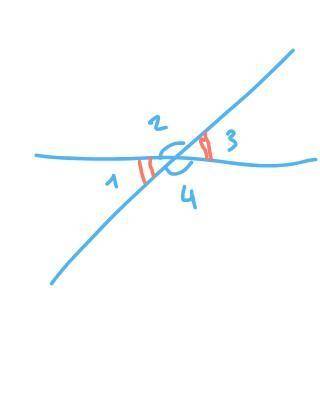
Вертикальные углы — у которых стороны одного угла являются продолжениями сторон другого угла. Вертикальные углы равны. Есть две пары вертикальных углов — ∠1 и ∠3, ∠2 и ∠4.
Смежные углы — два угла, у которых одна сторона общая, а две другие дополняют друг друга до прямой. Смежные углы в сумме равны 180°. Есть четыре пары смежных углов — ∠1 и ∠2, ∠2 и ∠3, ∠3 и ∠4, ∠1 и ∠4.
По условию, сумма трёх углов равна 196°.
∠1 + ∠2 + ∠3 = 196°.
∠1 и ∠2 — смежные углы, ∠1 + ∠2 = 180°, => ∠3 = 196° – 180° = 16°.
∠1 и ∠3 — вертикальные углы, ∠1 = ∠3 = 16°, => ∠2 = 196° – 16° – 16° = 164°.
Итого, ∠1 = ∠3 = 16°, ∠2 = ∠4 = 164°.
Меньший угол — ∠1 и ∠3 — равен 16°.
ответ: 16°.
Доказательство теоремы 4. Рассмотрим сначала случай, когда лучи, образующие данный угол, пересекают окружность каждый в двух различных точках (рис. 5).
Обозначим через O вершину угла, а точки пересечения лучей и окружности через A, B, C и D (A между O и B, C между O и D). Тогда
Первое равенство верно, так как в треугольнике OBC внешний угол BCD равен сумме двух внутренних углов, с ним не смежных.
Пусть теперь один из лучей (например, OA) касается окружности в точке A, а другой пересекает ее в точках B и C; B между O и C (рис. 6).