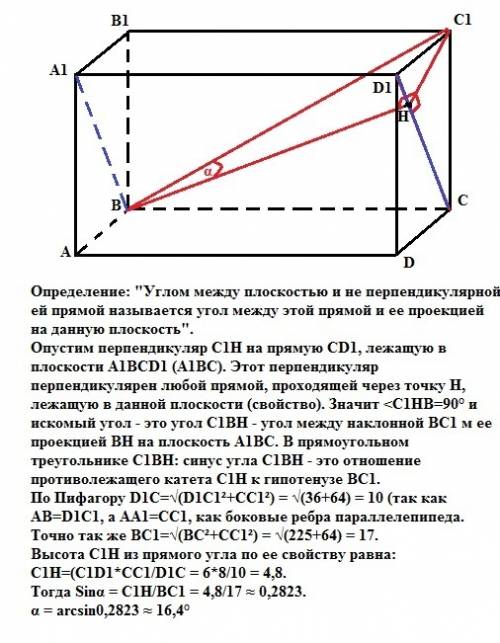
Определение: "Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость".
Опустим перпендикуляр С1Н на прямую СD1, лежащую в плоскости А1ВС (это плоскость А1ВСD1, так как секущая плоскость пересекает параллельные плоскости АА1В1В и DD1C1C по параллельным прямым А1В и D1C). Отрезок С1Н перпендикулярен любой прямой, проходящей через точку Н, лежащую в данной плоскости (свойство). Значит <C1HB=90° и искомый угол - это угол С1ВН - угол между наклонной ВС1 м ее проекцией ВН на плоскость А1ВС. В прямоугольном треугольнике С1ВН: синус угла С1ВН - это отношение противолежащего катета С1Н к гипотенузе ВС1.
По Пифагору D1C=√(D1C1²+CC1²) = √(36+64) = 10 ед (так как АВ=D1C1, a AA1=CC1, как боковые ребра параллелепипеда.
Точно так же ВС1=√(ВC²+CC1²) = √(225+64) = 17 ед.
Высота С1Н из прямого угла по ее свойству равна:
С1Н=(С1D1*CC1/D1C = 6*8/10 = 4,8 ед.
Тогда Sinα = C1H/BC1 = 4,8/17 ≈ 0,2823.
α = arcsin0,2823 ≈ 16,4°.
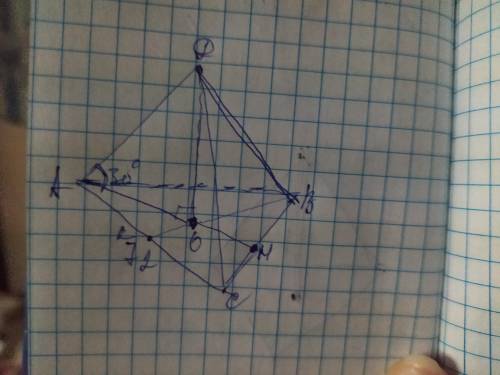
ответ: ДО=8√3см
Объяснение: обозначим вершины основания пирамиды А В С, вершину пирамиды Д, а её высоту ДО. В основании правильной трёхугольной пирамиды лежит равносторонний треугольник, поэтому АВ=ВС=АС=72м
Найдём площадь основания по формуле:
S=a²√3/4,где а- сторона основания:
S=72²√3/4=5184//√3/4=1296√3см²
S=1296см².
Проведём из вершин основания медианы АН и ВК. Они пересекаясь в точке О делятся между собой в отношении 2:1, начиная от вершины треугольника: АО: ОН=2:1. Также медиана является ещё и высотой, поскольку треугольник равносторонний. Найдём высоту основания через площадь следуя формуле обратной формуле площади:
S=½×a×h
h=S÷a÷½=1296÷72÷½=18×2=36см
h=36см
Обозначим пропорции 2:1 как 2х и х, и зная величину высоты, составим уравнение:
2х+х=36
3х=36
х=36/3
х=12
ОН=12см, тогда АО=12×2=24см.
Рассмотрим ∆АДО. Он прямоугольный где АО и ДО- катеты, а АД- гипотенуза. Угол ДАО=30°, по условиям, а катет лежащий напротив него равен половине гипотенузы, поэтому ДО=½× АД
Пусть ДО=х, тогда АД=2х, зная, что АО=24см, составим уравнение используя теорему Пифагора:
АД²-ДР²=АО²
(2х)²-х²=24²
4х²-х²=576
3х²=576
х²=576/3
х²=192
х=√192=√(3×64)=8√3
Итак: ДО=8√3см
т.е. a+b+c=180
1) c=180-(a+b)
по условию сумма двух внеш. углов и одного внутрен. (у разных вершин)=360
с+(180-a)+(180-b)=360 => c-a-b=0 => c=a+b
подставим в формулу №1 a+b=180-a-b => 2(a+b)=180 a+b=90
с=180-(a+b)=180-90=90
т.е. при данных условиях треугольник прямоугольный