Уравнение окружности радиуса R с центром в точке C (a; b) имеет вид:
(x – a)² + (y – b)² = R².
1. Радиус — расстояние от центра окружности до любой точки на окружности. Таким образом, радиус будет равен расстоянию от точки k (1; 2) до точки p (-3; 2).
Расстояние между точками A (x₁; y₁) и B (x₂; y₂) вычисляется по формуле:
AB = √((x₁ - x₂)² + (y₁ - y₂)²).
Таким образом, расстояние между точками k (1; 2) и p (-3; 2) будет равно:
kp = R = √(1+3)² + (2 - 2)²) = √(4)² + 0 = 4.
1. Подставим известные значения в уравнение окружности радиуса R = 4 с центром в точке k (1; 2):
(x – 1)² + (y – 2)² = 5²;
(x – 1)² + (y – 2)² = 25.
ответ: (x – 1)² + (y – 2)² = 25.
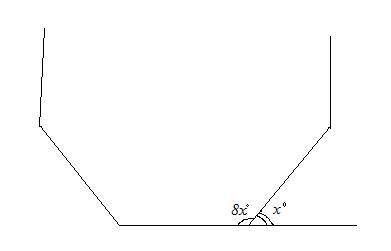
Внешний угол правильного многоугольника и его внутренний угол являются смежными, значит, их сумма равна 180°.
Т.к. по условию задачи внутренний угол в 8 раз больше внешнего, то пусть внешний угол х°, тогда внутренний угол будет равен (8х)° (см. рис.). Составим и решим уравнение:
х + 8х = 180.
9х = 180,
х = 180 : 9,
х = 20.
Значит, внутренний угол правильного многоугольника равен
8 · 20° = 160°.
Внутренний угол правильного многоугольника находят по формуле:
180° · (n - 2) / n, где n - число сторон правильного многоугольника.
Имеем:
180° · (n - 2) / n = 160°,
180° · (n - 2) =160° · n,
9 · (n - 2) = 8 · n,
9n - 18 = 8n,
9n - 8n = 18,
n = 18.
Значит, наш правильный многоугольник имеет 18 сторон.
ответ: 18 сторон.
Тогда,
Р=3*а; где а-сторона треугольника.
8,1=3*а
а=8,1:3
а=2,7
Теперь находим среднюю линию треугольника:
Ср.=а:2=2,7:2=1,35
ответ: 1,35 дм