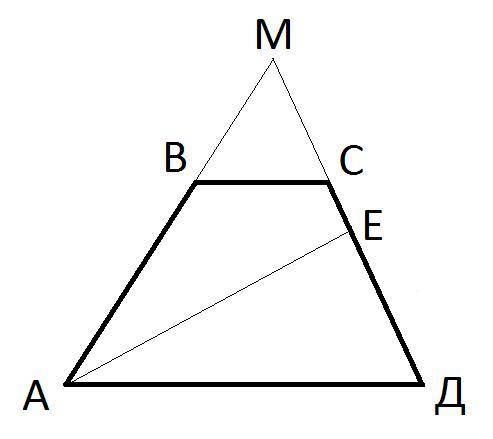
Смотрите рисунок. Продолжим стороны АВ и ДС до их пересечения между собой получим точку М. Поскольку биссектриса <А перпендикулярна СД, то она – биссектриса перпендикулярна и ДМ. Следовательно, треугольник АДМ - равнобедренный. И АД = АМ. Впрочем, это не важно. Но раз треугольник АДМ равнобедренный, а АЕ перпендикуляр на ДМ, то ДЕ = МЕ = 5. Тогда МС = МЕ-СЕ = 5 – 1 = 4. Следовательно, МД = МС + СЕ + ЕД = 4 + 1 + 5 = 10. Поскольку АД и ВС параллельны между собой, то треугольники ВМС и АМД - подобны. Из подобия этих треугольников вытекает, что АД/ВС = МД/МС = 10/4 = 5/2
Zmeura1204
Объяснение:
1)
Дано:
АВСD-параллелограм
AB=10см
AD=15см
<А=30°
S=?
_______
Решение
S=AB*AD*sin<A
sin<30°=1/2
S=1/2*10*15=75см²
ответ: 75см²
2)
Дано:
ABCD- трапеция
<ВАD=<ABC=90°
<BCD=135°
BC=2см
АВ=2см
S(ABCD)=?
______
Решение
Сумма углов прилежащих к боковой стороне трапеции равна 180°
<CDK=180°-<BCD=180°-135°=45°
Проведём высоту СК.
∆CKD- прямоугольный равнобедренный треугольник (углы при основании равны. <СКD=90°; <CDK=45°; <KCD=90°-45°=45°)
CK=KD=AB=2см
АD=BC+KD=2+2=4см.
S(ABCD)=CK(BC+AD)/2=2(2+4)/2=6см²
ответ: 6см²