1 повторник изученного в 5 КЛАССЕ»
1. Прочитаите кст
(1) Xout ) n рус) на аные анимы
(2) Груеке сперка от масие об у скрие (подоn дом
бе не иман морихое утро на крышами деревенских
aerononoaмa ne na
мі) і енемнои шу бои набе,
на у на
(0)
teen е
нива енее оним светом, снят луна .
(0) В номере мают по дерев ее. (0) Хорошо ае, адна
накатана имота е Ten rем в nety (11) Креnок зимний
немен моро отросконалот во устаолы дерев en (12) Высокие
ana na na но не
(13) Про се оn an am с неи 11 оно зае део ,
ука и на
span npornурса по небу Млеч. и
Путанало на весна
5 в Мелом пути распростер
свое полошо
(1а антастическое казено есть в лунно зимна ночи (17)
Ben минало спушки не саха оголевские рассеказы Toneron Бунин .
(1) Кому прих ал. л. nyo o o o мн м просеnочным
дорога (не) ауапон не
119) A a you un pa
оняна когда покрытые снегом
nondoniopan und door wtorie не с аншего сонца и забаста
аас оr nеn аn
Bononato

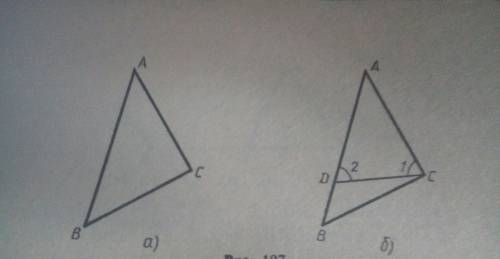
ΔABC,
ΔA1B1C1,
AB=A1B1, ∠A=∠A1, ∠B=∠B1.
Доказать:
ΔABC= ΔA1B1C1
Доказательство:
Так как AB=A1B1, то треугольник A1B1C1 можно наложить на треугольник ABC так, чтобы
сторона A1B1 совместилась со стороной AB,точки C1 и С лежали по одну сторону от прямой AB.
Поскольку ∠A=∠A1, сторона A1С1 при этом наложится на луч AC.
Так как ∠B=∠B1, сторона B1C1 наложится на сторону BC.
Точка С1 принадлежит как стороне A1С1, так и стороне B1C1, поэтому С1 лежит и на луче AC, и на луче CB.
Лучи AC и CB пересекаются в точке C. Следовательно, точка С1 совместится с точкой C.
Значит, сторона A1С1 совместится со стороной AC, а сторона B1C1 — со стороной BC.
Таким образом, при наложении треугольники ABC и A1B1C1 полностью совместятся.
А это означает, что ΔABC= ΔA1B1C1 (по определению).
Что и требовалось доказать.