Дано: h=10см, S(б)=40см^2
Найти:
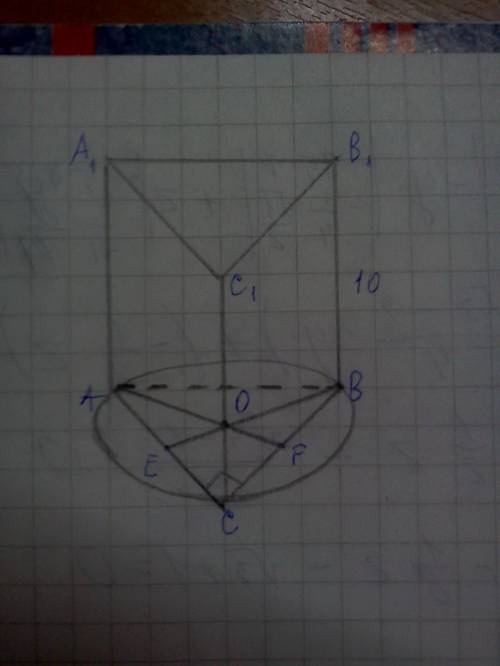
Делаем рисунок. Рисовать весь описаный цилиндр не обезательно, нас интересует лишь основа цилиндра.
Найдем отношение сторон друг к другу (в треугольнике ABC)
Т.к. это равнобедренный прямоугольный треугольник, то углы CAB и CBA равны 45 градусам. 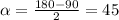
Зная угол можем сказать
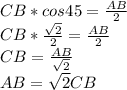
Затем записываем формулу для площади боковой поверхности
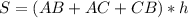
AC заменяем на CB, AB заменяем на √2*CB и решаем как уравнение с неизвестной
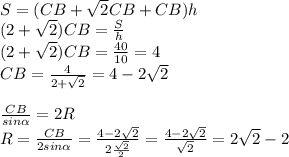
Пусть АВСД-равнобедренная трапеция. АС=10-диагональ, Угол САД=60.
Опустим из вершины С высоту СН к стороне АД. В прямоугольном треугольнике АСН угол АСН=180-угол СНА (=90, та как СН-высота)-угол САН(он же САД)=180-90-60=30. Против угла в 30 градусов лежит катет АН равный половине гипотенузы АС. АН=10/2=5. По теореме Пифагора найдем высоту СН=АС в квадрате-АН в квадрате все под корнем=10 в квадрате-5 в квадрате все под корнем=5 корней из 3. В равнобедренной трапеции высота (СН=5 корней из 3) равна полусумме оснований. А площадь равна произведению полусуммы оснований на высоту. S=5 корней из 3*5корней из 3=75
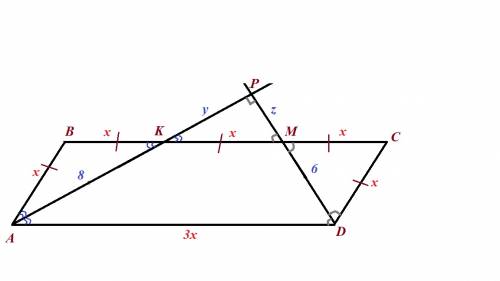
Чертеж к решению - во вложении.
Известно, что биссектрисы двух непротивоположных углов параллелограмма пересекаются под прямым углом и отсекают равнобедренные треугольники. Таким, образом, треугольники АВК и МСД равнобедренные, а треугольник КРМ - прямоугольный.
Все равные углы (накрест лежащие и вертикальные), а также равные отрезки отмечены на чертеже.
Ведем обозначения: ВК=КМ=МС=х, КР=у, МР=z.
Периметр параллелограмма P=2(АВ+ВС)=8х.
Треугольники РАД и РКМ подобны по двум углам. Поэтому
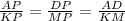
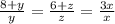
1) 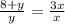
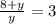
3y=8+y
y=4,
2) 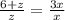
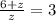
z+6=3z
z=3,
По теореме Пифагора в треугольнике КРМ
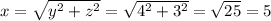
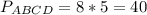
ответ: 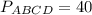
Цилиндр описанный, => прямоуг.треуг.вписан в окружность, => R равен половине гипотенузы
треугольник равнобедренный, по т.Пифагора
(2R)^2 = 2x^2, где x---катет
R^2 = x^2 / 2
R = x / корень(2)
Sбок.призмы = высота * (x+x+гипотенуза) = 40
2x + 2R = 40/10 = 4
x+R = 2
x = 2-R
R = (2-R) / корень(2)
2-R-Rкорень(2) = 0
2-R(1+корень(2)) = 0
R = 2 / (1+корень(2))
можно избавиться от иррациональности в знаменателе:
домножить числитель и знаменатель на сопряженное выражение (1-корень(2))
R = 2(1-V2) / ((1-V2)(1+V2)) = 2(1-V2) / (1-2) = 2(корень(2) - 1)