Задача с таким условием наверняка дается с рисунком, который должен быть приложен.
ответ: а) 24,2 м²; б) 34,848 м²; в) 8,712 м²
Объяснение:
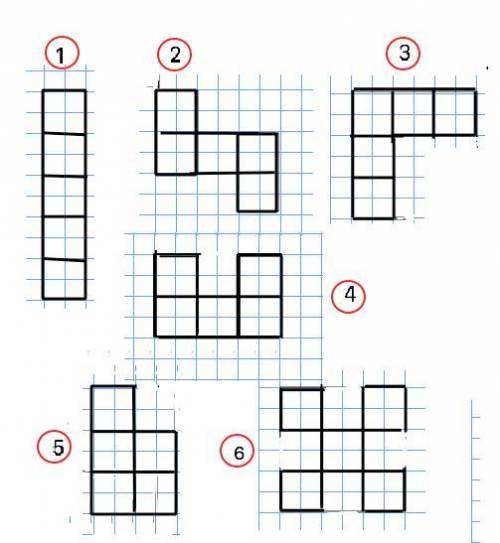
Количество n свободных сторон, участвующих при измерении периметра, при различном расположении пяти квадратных участков двора может быть разным. (см. рисунок приложения)
Тогда длина стороны квадрата а=P:n, Ѕ (двора)=5•а²
а) № 1, 2, 3, 4 – n=12 ⇒ a=2640:12=220 cм=2,2 м ⇒ Ѕ=5•2,2² =24,2 м²
б) №5 – n=10. ⇒ а=2,64м ⇒ Ѕ= 5•2,64² =34,848 м²
в) №6 – n=20 ⇒ а=1,32 м ⇒ Ѕ=5•1,32² =8,712 м²
Расстояние между прямой и плоскостью (если они || ) - перпендикуляр, опущенный из любой точки прямой на плоскость. Например: A1 лежит на прямой A1B1 и на плоскости AA1C1C, а плоскость AA1C1C пересекается с плоскостью сечения по прямой AC1, прямая AC1 лежит и в плоскости ABC1, т.е. искомое расстояние - перпендикуляр A1P к прямой AC1 (аналогично можно рассмотреть точку B1 и прямую BC1... расстояние будет то же самое...)
AA1C1C - прямоугольник со сторонами 6 и 3, AC1 - его диагональ, искомый отрезок A1P - это высота к гипотенузе в прямоугольном треугольнике AA1C1.
Этот отрезок можно найти или через площадь треугольника AA1C1 (с одной стороны площадь прямоуг.треуг.равна половине произведения катетов, с другой стороны - половине произведения AC1 на A1P) или из подобия прямоугольных треугольников AA1C1 и PA1C1 (у них еще общий угол C1 - подобие по двум углам): A1P : 3 = 6 : AC1
A1P = 18/AC1
AC1^2 = 6*6+3*3 = 36+9 = 45
AC1 = 3корень(5)
A1P = 18/3корень(5) = 6/корень(5) = 6/5 * корень(5) = 1.2 * корень(5)