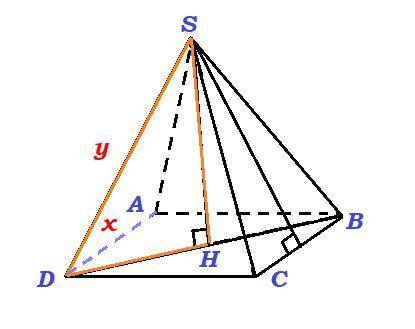
Правильная четырёхугольная пирамида SABCD;
Сторона основания AD =  ;
;
Боковое ребро SD = 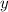 .
.
V = ?
Решение: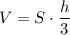
Поскольку в основании правильной четырёхугольной пирамиды лежит квадрат, то S основания = Ѕ квадрата = 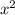
Вершина высоты правильной пирамиды проецируется в центр ее основания - здесь это точка пересечения диагоналей квадрата.
Высоту h пирамиды найдём из прямоугольного треугольника SHD, гипотенуза которого равна боковому ребру пирамиды, a катет DH равен половине диагонали основания.
Диагонали квадрата равны.
⇒ 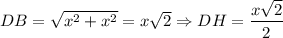
Найдём 2 катет по т.Пифагора (он же высота пирамиды):
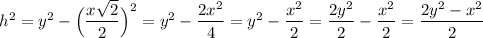
Отсюда: 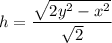 .
.
Остаётся найти ответ на вопрос: чему равен объём пирамиды.
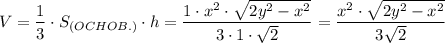 .
.
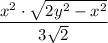
1) пусть одна сторона будет Х ( а их две) , а вторая (мы знаем из условия) =9 (их тоже две)
зная периметр ,найдем сторону
Х+Х+9+9=26
2Х+18=26
2Х=26-18=8
Х=4
2) зная что одна сторона =4, а вторая =9 ,найдем площадь прямоугольника
9 умножить на 4 = 36
3)мы знаем что площадь квадрата (равна площади прямоугольника ) = 36
Т.к. в квадрате стороны равны и мы знаем что площадь =36, то одна сторона квадрата будет равна корню их 36 т.е. = 6
( 6 на 6 =36 )
ответ :сторона квадрата =6