Выразим через Х одну из двух равнобедренных сторон, тогда Х+8 сторона, лежащая противи тупого угла.
Составляем уравнение.
Х+Х+Х+8=38
3Х=30
Х=10
ответ: Стороны треугольника равны 10, 10 и 18 см.
9.
<MBA = 120° => <CBA = 180-120 = 60°.
<CBA = 60° => <A = 90-60 = 30°.
Теорема о 30-градусном угле такова: катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы.
Тоесть: BC = AB/2.
У нас есть 2 условия: BC = AB/2; BC+AB = 36.
Составим из этих условий систему уравнений, с переменными: BC = x; AB = y.
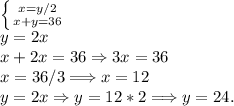
Вывод: AB = 24; BC = 12.
10.
Так как все стороны равны, то треугольник — равносторонний, тоесть каждый из внутренних углов равен: 180/3 = 60°.
MP == PK = MK/2 = 13/2 = 6.5.
PK = 6.5(гипотенуза)
<K = 60° ⇒ <RPK = 90-60 = 30°.
По теорема о 30-градусном угле: RK = PK/2 = 6.5/2 = 3.25.
RK = 3.25; NK = 13 => NR = 13-3.25 = 9.75.
Вывод: NR = 9.75.
Пусть длина равна a, ширина b. Площадь ab=3600, периметр 2(a+b), нужно найти минимум периметра, то есть минимум функции p=2(a+b). Из формулы для площади выражаем a=3600/b и подставляем в формулу для периметра p=2(a+b), получаем p=2((3600/b)+b)=(7200/b)+2b, находим производную (производная суммы двух слагаемых) и приравниваем её к нулю (ибо нам нужен минимум): dp/db=(-7200/(b^2))+2, решаем уравнение, получаем (b-60)(b+60)=0, два корня: b=60 или b=-60, второй не подходит, длина всегда неотрицательна, первый подходит, его подставляем в формулу для а, получаем а=60, ответ: (60м) х (60м).
Объяснение:
Пусть х-большая сторона, а у-две равные боковые стороны, то:
х-у=8
2у+х=38
Выражаем из первого ур-ния х, х=8+у, подставляем во 2 ур-ние, получится:
2у+8+у=38
3у=30
у=10
х=18
ответ: 10 см, 10 см, 18 см