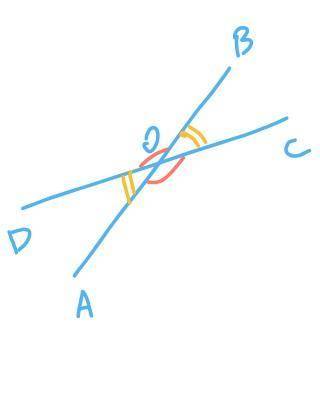
При пересечении двух прямых образовались вертикальные углы (стороны одного угла являются продолжениями сторон другого угла), это ∡AOD и ∡BOC, ∡BOD и ∡AOC. Вертикальные углы равны => ∡AOD = ∡BOC, ∡BOD = ∡AOC.
Также образовались смежные углы (два угла, у которых одна сторона общая, а две другие дополняют друг друга до прямой), это ∡AOD и ∡BOD, ∡BOD и ∡BOC, ∡BOC и ∡AOC, ∡AOC и ∡AOD. Сумма смежных углов равна 180°.
По условию задачи, углы, которые нужно найти, не могут быть вертикальными (по условию углы не равны), значит это пара смежных углов.
Допустим, что ∡AOD на 20° меньше ∡AOC => ∡AOD = ∡AOC – 20°.
∡AOD + ∡AOC = 180°,
∡AOC – 20° + ∡AOC = 180°,
2 × ∡AOC = 200°,
∡AOC = 200° ÷ 2 = 100°;
∡AOD = ∡AOC – 20° = 100° – 20° = 80°
ответ: 100° и 80°
Вектор АС(-2;y-5;-8). Модуль вектора (его длина) |AC|=√(4+(y-5)²+64).
Вектор ВС(-6;(y-1);0). Модуль вектора (его длина) |BC|=√(36+(y-1)²+0).
Модули (длины) этих векторов равны по условию. Значит
√(4+(y-5)²+64)=√(36+(y-1)²+0).
Возведем обе части в квадрат:
4+(y-5)²+64=36+(y-1)² или
4+y²-10y+25+64=36+y²-2y+1
8y=56.
y=7.
ответ: С(0;7;0)
Проверим: |AC|=√(4+4+64)=√72, |BC|=√(36+36+0)=√72.
То есть точка С находится на равном расстоянии (равноудалена) от точек А и В.