А1.по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов квадрат гипотенузы равен 3^2+4^2=25
гипотенуза равна корень(25)= 5 см
ответ: 5 см
А2.вводим переменную x
2x-одна сторона
3x-смежная с ней
сторона MK равна 2x а сторона KP 3x гипотенуза 5
по теореме Пифагора a²+b²=c²
(2x)²+(3x)²=5
4x²+9x²=5
13x²=5
x²=5÷13
x=√5÷13
меньшая сторона 2x =2×√5÷13
А3.Внутренний угол C=180-150=30
Тут 2 случая:
1). В=90
Пусть АВ =х . Катет, лежащий против угла 30 градусов равен половине гипотенузы:
Значит, АС= 2х
Тогда 2х=х=4; х=4
ответ: АВ=4
2).А=90
Пусть АВ =х . Катет, лежащий против угла 30 градусов равен половине гипотенузы:
Значит, ВС= 2х
Тогда 2х=х=4; х=4
ответ: АВ=4
А4.рассмотрим ΔВОС. в нем ОВ=6/2=3
ОС=8/2=4 т.к диагонали делятся пополам в месте пересечения
∠ВОС=90°, т.к диагонали перпендикулярны по св-ву.
ВС-? , ⇒
по т пифагора
ВС²=ОВ²+ОС²
ВС²=9+16
ВС²=25
ВС=5
1.
Пусть дан ABCD - прямоугольник, SАВСD = 15 см, АВ = 5 см.
Найдём ВС - ?
По формуле для Sпрямоуг = a×b ⇒ Sпрямоуг = AB×BC
BC=Sпрямоуг /AB
ВС=15/5 = 3 см
ответ : ВС = 3 см
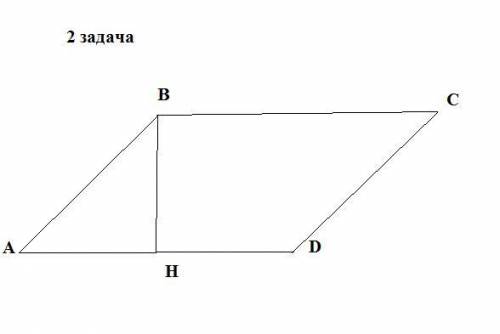
2.
Пусть дан параллелограмм ABCD,∠В= 150°, две стороны 12 и 16 см. Найдём SABCD -?
Из вершины В проведём высоту ВН к стороне АД.
∠А = 180° - ∠В = 180° - 150° = 30°.
Рассмотрим △АВН : ВН является высотой и катетом и находится против ∠30°.
АВ-гипотенуза , значит ВН = АВ : 2 = 12 : 2 = 6 см.
SABCD = ВН × АД = 6 × 16 = 96 см².
ответ : SABCD = 96 см²
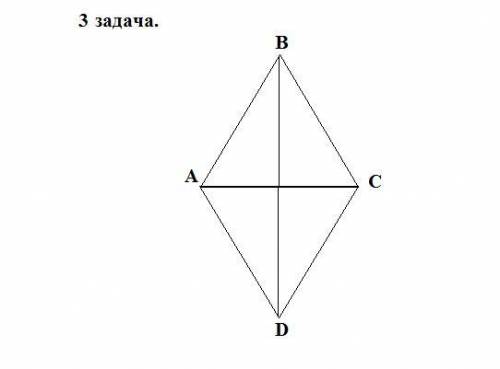
3.
Пусть дан ромб АВСD , АС- диагональ , ∠АСD = 35° .Найдём ∠АВС - ?
АС - биссектриса, ∠АСD = ∠ВАС = 35°, как накрестлежащие.
Рассмотрим △АВС : равобедренный, т.к у ромба все стороны равны, значит углы при основании равны.
∠АВС=180° - 35° - 35° = 110°
ответ : 110°
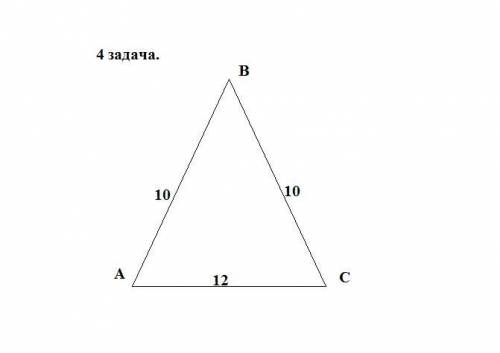
4.
Пусть дан △АВС-равнобедренный , АС-основание = 12 см.
АВ=ВС=10 см. Найдём S△АВС-?
Рассмотрим △АВС : Проведем высоту ВН , △АВС-равнобедренный ⇒ ВН является высотой , медианой и биссектрисой. Образован прямоугольный треугольник АВН, АН = НС = 12/2 = 6 см.
По теореме Пифагора найдём катет ВН :
ВН=√АВ² - АН²
ВН=√64
ВН=8 см
S△АВС=(ВН×АС)/2
S=(8×12)/2
S=48 кв. см
ответ:48 кв.см.
6.
2,4

В прямоугольном треугольнике высота, проведенная к гипотенузе, равна отношению произведения его катетов к гипотенузе
высота трапеции состоит из двух отрезков---высот подобных прямоугольных треугольников
обозначим катеты меньшего треугольника---x,y
из подобия этих треугольников: x : корень(3)-x = y : (1-y)
x*(1-y) = y*(корень(3)-x)
x-x*y = y*корень(3) - y*x
x = y*корень(3)
тогда по т.Пифагора гипотенуза = корень(x^2+y^2) = корень(3*y^2+y^2) = корень(4y^2) = 2y
аналогично в бОльшем треугольнике гипотенуза1 = корень((1-y)^2+(V3-x)^2) = 2*(1-y)
h = x*y/2y = x/2
h1 = (1-y)*(V3-x) / 2*(1-y) = (корень(3)-x)/2
высота трапеции = h+h1 = x/2 + (корень(3)-x)/2 = (x+корень(3)-x)/2 = корень(3)/2
Можно использовать тригонометрию, если знаетет...
x/y = ctg A = корень(3) => угол A = 30 градусов и, если рассмотреть прямоугольный треугольник, связывающий высоту трапеции и ее диагональ, то катет против угла в 30 градусов = половине гипотенузы... Решение гораздо короче.