на фото ответ
Объяснение:
второе задание:
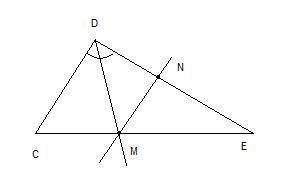
1. После построения MN получается треугольник MNE, подобный треугольнику CDE по первому признаку подобия (угол Е - общий, углы С и NME равны как соответственные углы при пересечении двух параллельных прямых CD и MN секущей СЕ). Поскольку треугольники подобны, то
<MNE = <CDE = 68°
2. Зная, что развернутый угол равен 180°, находим угол DNM:
<DNM = 180 - <MNE = 180 - 68 = 112°
3. Поскольку DM - биссектриса, то угол MDN = <CDE : 2 = 68 : 2 = 34°
4. Зная два угла треугольника DMN, находим неизвестный угол:
<DMN = 180 - <MDN - <DNM = 180 - 34 - 112 = 34°

Объяснение:
ABCD-параллелограмм⇒∠C=∠A, AD║BC
∠C=∠A⇒sin∠C=sin∠A
AD║BC⇒∠CBD=∠ADB
BE⊥AD⇒∠BED=90°
BF⊥AD⇒∠BFD=90°
∠BED=∠BFD=90°⇒ точки B,E,F,D лежат на одной окружности с диаметром BD. Тогда по теореме о равенстве вписанных углов имеем ∠BEF=∠BDF, ∠BDE=∠BFE
∠BFE=∠BDE=∠CBD
∠BEF=∠BDC, ∠BFE=∠CBD⇒ΔBEF~ΔBDC ч.т.д.
Из ΔBEF по теореме синусов имеем EF/sinEBF=2R, где R-радиус описанной окружности около ΔBEF⇒ R=0,5BD, так как это та самая окружность которая содержит точки B,E,F,D.
EF/sinEBF=2R⇒EF=2RsinEBF=BDsinC=BDsinA=15·0,4=6
Случаи того что угол В острый или тупой разбираются аналогично.