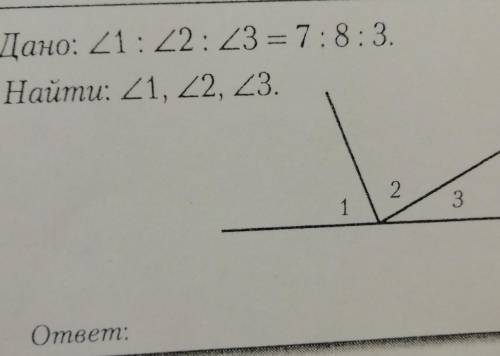
37. Решение:
∠1=65° (как вертикальные)
∠1 и угол в 65° равны, как соответственные углы при пересечении двух прямых секущей. Отсюда прямые параллельны. Значит ∠2=78° (как соответственные)
Поскольку сумма смежных углов равна 180°, то
х=180°-∠2=180°-78°=102°
ответ: 102°
38. Решение (аналогично):
∠1=70° (как вертикальные)
∠1 и угол в 70° равны, как соответственные углы при пересечении двух прямых секущей. Отсюда прямые параллельны. Значит ∠2=50° (как соответственные)
х=∠2 (как вертикальные)
х=50°
ответ: 50°
(Чертёж в приложении)
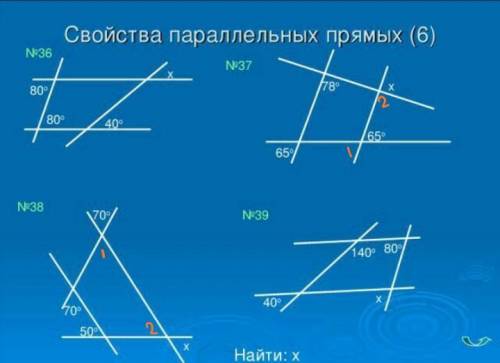
угол 1 = 70°, угол 2 =80°, угол 3 = 30°
Объяснение:
угол 1 = 7х, угол 2 = 8х, угол3 = 3х
так как они в отношении 7:8:3
далее:
составляем уравнение, так легче
если сложить все углы, то получиться 180°
из этого получаем
угол 1 + угол 2 + угол 3 = 180
подставляем значения
7х+8х+3х=180
18х=180
х=10
теперь вместо х, подставляем 10, и находим углы
угол 1= 7•10=70°
угол 2= 8•10=80°
угол 3= 3•10=30°