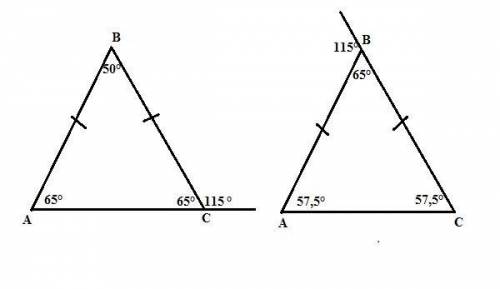
1. 65°, 65°, 50°.
2. 57,5°; 57,5°; 65°.
Объяснение:
Нам дан один из внешних углов равнобедренного треугольника. У равнобедренного треугольника углы при основании равны.
Значит возможны два варианта решения:
1. Если дан внешний угол при основании, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Тогда угол при вершине треугольника равен 180° - 2·65° = 50° (по сумме внутренних углов треугольника, равной 180°).
ответ: 65°, 65°, 50°.
2. Если дан внешний угол при вершине, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Внешний угол треугольника равен сумме двух внутренних (в нашем случае равных), не смежных с ним углов. Следовательно, углы при основании такого треугольника равны 115°:2 = 57,5°.
ответ: 57,5°; 57,5°; 65°.
1. a = 2*i - j + 4*k; b = 3*i - 3*k;
2*a + b = 7*i - 2*j + 5*k;
a - b = -i - j +k;
(2*a + b)*(a - b) = -7 + 2 + 5 = 0;
2. dc + 2*d^2 = 3*4*cos(60) + 2*16 = 38;
3. ab = -2 + 12*α = 0; α = 1/6;
4. 3*c + b = (5, -2, 5); I3*c + bI = корень(5^2 + 2^2 + 5^2) = 3*корень(6);
5. ab/(IaI*IbI) = (-3 + 4 + 3)/корень(( 9 + 4 + 1)*(1 + 4 + 9)) = 2/7;
6. m = -3; n = 3; в этом случае c = -d, других вариантов нет, поскольку проекции на ось z не зависят от m и n.
Проверьте арифметику!