1)
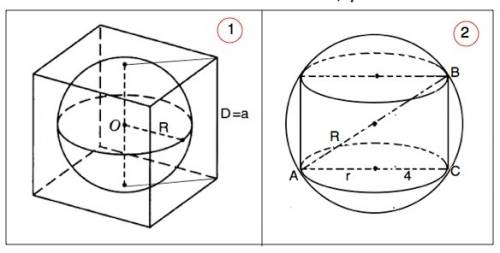
Диаметр вписанного в куб шара равен длине ребра куба, а радиус - половине длины ребра.
Площадь полной поверхности куба равна сумме площадей его 6-ти граней.
Площадь одной грани равна а² =1170/π :6=195/π
R²= (a/2)²=195/4π
Из формулы площади поверхности шара
S=4πR²=4π•195/4π=195 (ед. площади)
2)
Окружности, ограничивающие основания вписанного цилиндра изнутри касаются шара.
Осевое сечение цилиндра - прямоугольник, проходит через центр шара, при этом диаметр шара является диагональю этого прямоугольника.
Из формулы площади поверхности сферы 4πR²=100π находим её радиус R=5 ⇒ D=10
Диаметр основания цилиндра d=2r=8.
Из прямоугольного ∆ АВС высота ( образующая) цилинда ВС=6 ( по т.Пифагора или обратив внимание на отношение катета АС и гипотенузы АВ 4:5 - отношение сторон "египетского" треугольника)
Высота цилиндра - 6 ед. длины.
Треугольник АКС прямоугольный по теореме о трех перпендикулярах:
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной.
Проекция наклонной КС - катет ВС прямоугольного треугольника АВС с прямым углом С.
Угол КСА=90°
Чтобы найти площадь ⊿АКС, надо найти длину его катетов КС и СА.
СА - катет равнобедренного прямоугольного треугольника АСВ.
Гипотенуза АВ=4√2, следовательно, АС=ВС=4 ( по формуле диагонали квадрата
d=а√2, т.к. АСВ - половина квадрата с диагональю АВ) и а=4
Можно найти катеты и по теореме Пифагора с тем же результатом.
КС найдем по теореме Пифагора из треугольника КВС
КС²= КВ²+ВС² =36+16=50
КС=5√2
S ⊿АКС =4*5√2=20√2
------------
Перпендикулярными являются плоскости треугольников КВС и АВС