Объяснение:
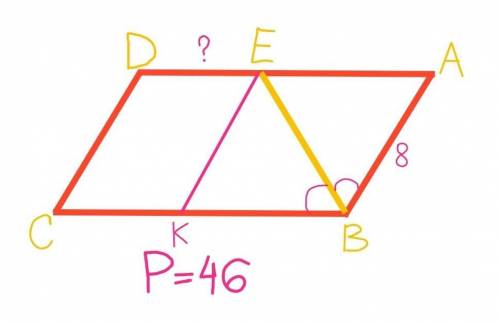
Из точки Е проведем отрезок ЕК, параллельный АВ.
Противоположные стороны параллелограмма параллельны, тоесть СВ//DE => ЕА//КВ и DE//CK
Так как в четырехугольнике КЕАВ стороны попарно параллельны, следовательно КЕАВ – параллелограмм.
ВЕ – биссектриса угла КВА по условию и диагональ параллелограмма КЕАВ.
Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм – ромб.
Следовательно: КЕАВ – ромб
У ромба все стороны равны. Исходя из этого: ЕА=КВ=АВ=8 см.
СD=AB=8 так как противоположные стороны параллелограмма равны.
Р(АВСD)=АВ+ВС+CD+AD=AB+BK+KC+CD+DE+EA=8+8+KC+8+DE+8=32+KC+DE
Так как Р(ABCD)=46 см по условию, то получим уравнение:
32+КС+DE=46
KC+DE=14 см
Так как ЕК//АВ, а АВ//CD, то ЕК//CD;
DE//CK (доказано ранее);
Исходя из этого: CDEK – параллелограмм.
Противоположные стороны параллелограмма равны, тоесть DE=CK.
Тогда 2DE=14 см
DE=7 см
ответ: 7 см
СD=10 см.
Диагональ АС является гипотенузой прямоугольного треугольника АВС, у которого катеты АВ и ВС.
Диагональ BD является гипотенузой прямоугольного треугольника АВD, у которого катеты АВ и AD.
Так катет ВС меньше катета AD, то и гипотенуза АС меньше гипотенузы BD.
АС=СD=10 cм.
Треугольник АСD - равнобедренный. Высота СК является одновременно и медианой.
СК=АВ=6 см
По теореме Пифагора из треугольника АСК:
АК²=АС²-СК²=10²-6²=100-36=64=8²
АК=8
АD=2·AK=16 см
BC=AK=8 cм
О т в е т. 8 см и 16 см.