Площадь полного круга занимает все его 360°.
Для ответа на заданный вопрос нужно найти, какую часть от целого круга составляет сектор с центральным углом, равный данным дугам. Такова же будет и часть площади, которую этот сектор занимает в круге.
Чтобы вычислить, какую часть целого числа составляет другое число, нужно представить ответ в виде правильной дроби. Записываем искомую величину над дробной чертой, как числитель а целое - под ней ( знаменатель). Желательно по возможности ( и для наглядности) сократить дробь (то есть разделить числитель и знаменатель на общий множитель.
а)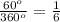
Какую часть от целого круга составляют оставшиеся три сектора и сектор с любой градусной мерой центрального угла, Вы без труда найдете самостоятельно.
Углы данной величины чаще всего встречаются в задачах по геометрии, и их доля от общего круга запоминается наизусть.
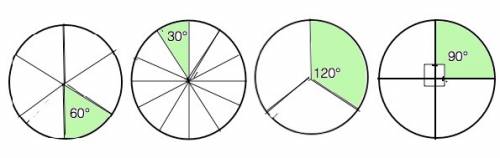
СН = корень (ВС в квадрате - ВН в квадрате) = корень (25 - 1) = корень 24
АН/НС = НС/ВН
АН = (НС х НС) /ВН = ( корень 24 х корень 24 ) /1 = 24
АВ = АН+ВН = 24+1=25
Sin A= ВС/АВ=5/25=0,2